Случайная величина

Теория вероятностей изучает математические модели случайных явлений окружающего нас мира. Результат любого случайного эксперимента можно характеризовать качественно и количественно.

Качественный результат случайного эксперимента — случайное событие.

Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества числовых значений, — случайная величина.

Основной объект изучения в теории вероятностей − случайные величины.

Простейшая модель случайной величины − монета, на одной стороне которой написано число 10, а на другой − число 20. В эксперименте с такой монетой элементарными событиями являются выпадения 10 или 20 . Перед нами случайная величина x, принимающая два значения 10 или 20 с некоторыми вероятностями, скорее всего, с равными вероятностями 0.5. Вся эта информация адекватно отображается таблицей

 

x	10	20
p	0.5	0.5

 

Эта таблица представляет вероятностное пространство.

В верхней строке перечислены элементарные события (событие состоит в том, что случайная величина x принимает значение, указанное в клетке таблицы), нижняя – назначенная этому событию вероятностью

Совершенно естественно обобщение на случай произвольного числа значений. Теперь для нас случайная величина – таблица вида

x			…		…
p			…		…

Поскольку в первой строке перечислены все возможные в данном эксперименте значения случайной величины, то понятно, что для соответствующих этим значениям вероятностей справедливо , .

Определённая таким образом случайная величина называется дискретной случайной величиной.

Непрерывные случайные величины возникают как естественное обобщение дискретной случайной величины.

Представим себе, что с точностью до нанометра измерен рост всех жителей Земли и что не оказалось двух людей одного роста. Тогда распределение случайной величины – роста случайно выбранного землянина – это таблица, содержащая 7 000 000 000 значений, результатов наблюдений:

 

x		…
p		…

Каждое значение вероятности равно .

Работать с такой гигантской таблицей крайне неудобно.

Как всегда в подобных случаях «спасаемся» графикой.

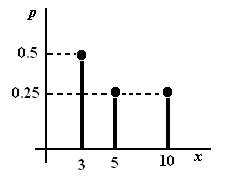
Например, распределение

x	3	5	10
p	0.5	0.25	0.25

 

можно изобразить в виде графика,

 

Для случайного роста землян получим что-то вида

то при большом, огромном, количестве значений случайной величины получим изображение получится

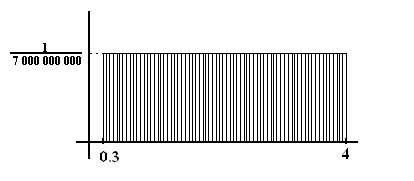
На отрезке [0.3, 4] (полагаем, что не бывает людей ниже 30 см и выше 4 м) расположено 7 000 000 000 «палочек».

Теперь разобьём отрезок [0.3, 4] на короткие отрезки, например длиной 1 мм (таких отрезков сколько?) и вычислим вероятность того, что рост случайно выбранного человека попадает в какой-то из таких промежутков – просуммируем количество «палочек» на каждом. Естественно, что в окрестности 2 м их будет больше, а возле 4 м не будет вообще.

По результатам суммирования построим новый график:

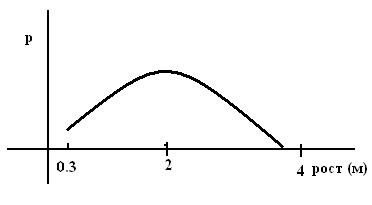
Понятно, что «на самом деле», например, если посмотреть в «микроскоп», график – ступенчатая фигура с шириной ступеньки в 1 мм.

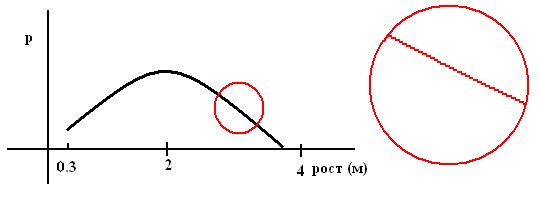
Также понятно, что в задаче о росте людей не будет больших ошибок, если вместо ступенчатого графика рассматривать гладкую непрерывную линию.

Этот график – изображение функции, которую называют плотностью распределения вероятностей непрерывной случайной величины и обозначают .

Эта функция имеет простой теоретико-вероятностный смысл:

если  плотность распределения вероятностей непрерывной случайной величиныx, то вероятность того, что случайная величина примет значение вблизи x,  вычисляется по формуле .

Отсюда сразу:

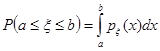  и .

Важно понимать, что плотность распределения случайной величины, это, образно говоря, «паспорт» случайной величины, в том смысле, что из неё можно извлечь всю информацию о случайной величине.

Заметим, что для дискретной величины таким «паспортом» является её распределение – таблица, о которой говорилось выше.

 

Формальное определение случайной величины может быть таким.

Случайной величиной называется действительная числовая функция x=x(w), wÎW, такая, что при любом действительном x .

Событие  принято записывать в виде x < x.

Случайные величины обычно обозначают  строчными греческими буквами x, h, z, …

Вот несколько примеров.

Пример 1. Подбросим монету один раз. Будем полагать «выигрыш» равным единице, если монета упала цифрой вверх и нулю, если она упала вверх гербом.

Случайное событие: монета упала цифрой или гербом вверх. Случайная величина — величина  «выигрыша».

Случайное событие: монета упала цифрой вверх. Значение случайной величины равно 1.

Случайное событие: монета упала гербом вверх. Значение случайной величины равно 0.

Эта случайная величина дискретная, она принимает значения из дискретного  множества {0, 1}.

Пример 2. Бросаем один раз игральную кость. Случайное событие — кость упала одной из граней вверх. Случайная величина — число, выпавшее на верхней грани.

Случайное событие — кость упала так, что на верхней грани одно очко. Значение случайной величины единица. Эта случайная величина дискретная, она принимает значения из дискретного  множества {1, 2, 3, 4, 5, 6}.

Пример 3. Бросаем один раз игральную кость. Случайное событие — кость упала одной из граней вверх. Если на верхней грани выпало меньше 3, полагаем «выигрыш» равным 0, если больше — 1, если выпало 3 очка — 2.

Случайное событие — на верхней грани 5. Значение случайной величины равно 1. Эта случайная величина дискретная, она принимает значения из дискретного  множества {0, 1, 2}.

Пример 4. На отрезке [0, 1] наугад (случайно) поставлена точка. Измеряется расстояние точки от левого конца отрезка. Полагаем случайную величину равной расстоянию от точки до левого конца отрезка.

Случайное событие — точка попала в середину отрезка, значение случайной величины 0.5.

Эта случайная величина непрерывная, она может принять любое значение из отрезка [0, 1], Пример 5. В урне красный, белый и чёрный шары. «Выигрыш» равен количеству белых шаров среди двух, выбранных наугад. Случайное событие — вынули красный и чёрный шар. Значение случайной величины 0. Эта случайная величина дискретная, она принимает значения из дискретного  множества {0, 1}.

Пример 6. Банк планирует инвестировать свободные средства в один из двух фондов. Один из фондов имеет  наибольшую доходность в период экономического подъёма, назовём его «Восход», другой — «Закат» — в период экономического спада. Оценивается доходность инвестиций для одного из трёх состояний экономики: подъём, стабильность, спад.  Данные даны в таблице:

Состояние экономики	Вероятность состояния	Доходность (прибыль на каждые вложенные 1000 $)
		«Восход»	«Закат»
Спад	0.2	– 100	+ 200
Стабильность	0.5	+100	+50
Подъём	0.3	+250	– 100

Случайное событие — состояние экономики. Случайная величина — доходность (средства вкладываются в тот фонд, который даёт наибольшую доходность).

Например, случайное событие — спад в экономике, значение случайной величины +200.