Проверка гипотезы о числовом значении математического ожидания при известной дисперсии
Пусть x — нормально распределенная случайная величина с неизвестным математическим ожиданием a и известной дисперсией Dx = s2, представленная выборочными значениями
x1, x2, …, xn.
Задача состоит в проверке гипотезы о том, что неизвестный параметр a равен заданному числу a0.
Пусть Mx = a — неизвестная величина, а дисперсия Dx = s2 — известна.
Сформулируем нулевую гипотезу H0 о том, что неизвестный параметр a равен заданному числу a0, т.е. H0: a=a0.
Альтернативную гипотезу H1 можно сформулировать тремя способами:
- H1: a¹a0;
- H1: a>a0;
- H1: a<a0.
Рассмотрим подробно каждый из этих трех случаев.
Двусторонняя альтернативная гипотеза: нулевая гипотеза H0: a = a0 , альтернативная гипотеза H1: a ¹ a0
Зададимся некоторым уровнем значимости a и по выборке 
вычислим значение критерия 
, где 
.
Критерий j сконструирован так, что если гипотеза H0 верна, то, во-первых, случайная величина j имеет стандартное нормальное распределение и, во-вторых, здравый смысл подсказывает, что в большинстве экспериментов величина j будет мало отличаться от нуля (поскольку 
, то разность 
мала, если верна гипотеза 
).
Если же отклонения 
от нуля велики, то это скорее всего указывает на ошибочность нулевой гипотезы.
Выделим для критерия j критическую область, т.е. укажем такие значения j, при которых гипотезу H0 следует отвергнуть.
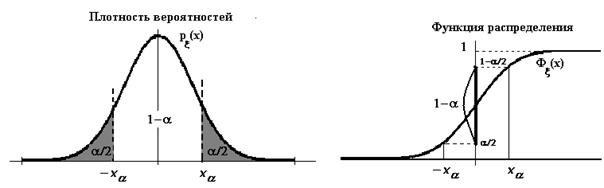
На рис.2 изображены плотность распределения случайной величины j (говорят «плотность распределения критерия j») и функция распределения, в данном случае для стандартного нормального распределения.
Границы критической области 
и 
определяются условиям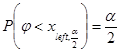и
и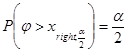 
.
Поскольку критерий 
имеет стандартное нормальное распределение, то правая точка 
является корнем уравнения
.
Здесь 
– функция Лапласа, функция распределения нормального закона 
, для которой справедливо
.
Левая точка 
расположена симметрично и вычисляется по формуле 
, поскольку 
и если 
, то 
.
Теперь, когда критическая область 
найдена, можно по выборке вычислить значение критерия j и проверить, попадает ли оно в критическую область.
Если 
, то с уровнем значимости 
гипотеза H0 принимается.
Если же 
или 
, то гипотеза H0 отвергается и принимается альтернативная гипотеза H1.
Пример 1
Пример 1. Задана выборка, содержащая 150 значений случайной величины, о которой известно, что она распределена нормальное, её математическое ожидание Mx = a неизвестно, но известна дисперсия Dx = s2= 0.1.
Задача состоит в проверке с уровнем значимости 
гипотезы H0: a = 10 при двусторонней альтернативной гипотезе H1: a ¹ 10.
На приведенном ниже рисунке изображён фрагмент листа Excel с решением задачи процедурой «Описательные статистики» пакета «Анализ данных».
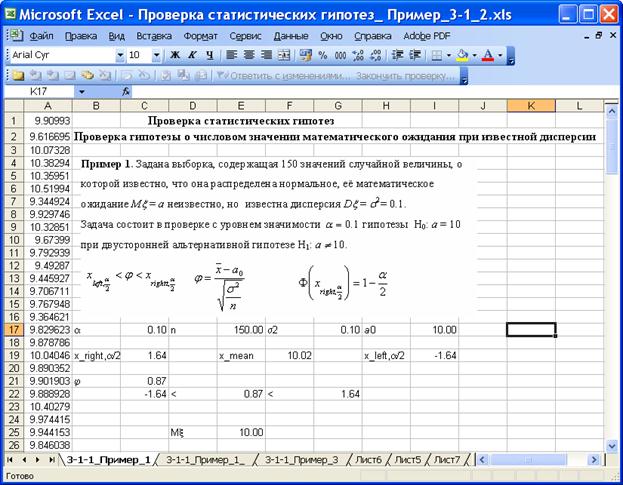
Значение критерия j = 0.87, область принятия нулевой гипотезы (- 1.64, 1.64), значение критерия попадает в область принятия нулевой гипотезы, - 1.64< 0.87<1.64, нулевая гипотеза H0: a = 10 принимается с уровнем значимости 0.1.
Важно помнить, что гипотеза проверялась в предположении о нормальности выборки.
Пример 2
Пример 2. Задана выборка, содержащая 150 значений случайной величины, о которой известно, что она распределена нормальное, её математическое ожидание Mx = a неизвестно, но известна дисперсия Dx = s2= 0.1.
Задача состоит в проверке с уровнем значимости 
гипотезы H0: a = 10 при двусторонней альтернативной гипотезе H1: a ¹ 10.
На приведенном ниже рисунке изображён фрагмент листа Excel с решением задачи.
Значение критерия j = – 77.10, критическая область (область отклонения нулевой гипотезы) — промежуток (– ¥, – 1.64)È(1.64, ¥).
Значение критерия попадает в критическую область, – 77.10< –1.64, следовательно, нулевая гипотеза H0: a = 10 отклоняется с уровнем значимости 0.1, принимается альтернативная гипотеза H1: a¹ 10.
Важно помнить, что гипотеза проверялась в предположении о нормальности выборки.
Пример 3
Пример 3. Задана выборка, содержащая 150 значений случайной величины, о которой известно, что она распределена нормальное, её математическое ожидание Mx = a неизвестно, но известна дисперсия Dx = s2= 0.1.
Задача состоит в проверке с уровнем значимости 
гипотезы H0: a = 10 при односторонней альтернативной гипотезе H1: a > 10.
Выборочные значения записаны в ячейках A1:A150 (Файл Excel …)
На приведенном ниже рисунке изображён фрагмент листа Excel с решением задачи.
Значение критерия j = 0.87, область принятия нулевой гипотезы (– ¥, 1.28), значение критерия попадает в область принятия нулевой гипотезы, 0.87<1.28, нулевая гипотеза H0: a = 10 принимается с уровнем значимости 0.1.
Важно помнить, что гипотеза проверялась в предположении о нормальности выборки.
Пример 4
Пример 4. Задана выборка, содержащая 150 значений случайной величины, о которой известно, что она распределена нормальное, её математическое ожидание Mx = a неизвестно, но известна дисперсия Dx = s2 = 0.1.
Задача состоит в проверке с уровнем значимости 
гипотезы H0: a = 10 при односторонней альтернативной гипотезе H1: a > 10.
На приведенном ниже рисунке изображён фрагмент листа Excel с решением задачи.
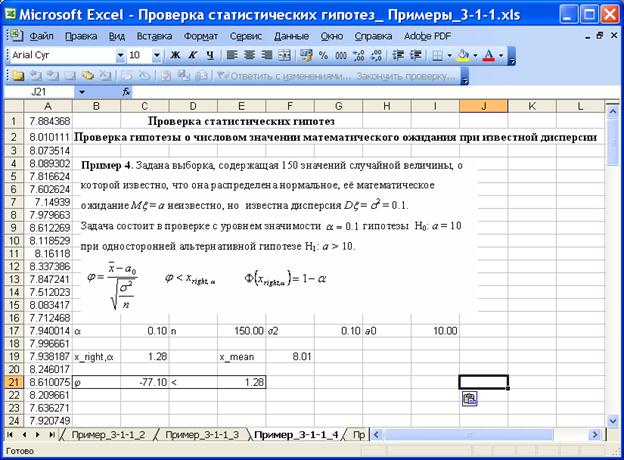
Значение критерия j = – 77.10, область принятия нулевой гипотезы (– ¥, 1.28), значение критерия попадает в область принятия нулевой гипотезы, – 77.10, нулевая гипотеза H0: a = 10 принимается с уровнем значимости 0.1.
Если внимательно посмотреть на гистограмму, на описательные статистики (Среднее = 8.01 — точечная оценка математического ожидания), то станет понятно, что результат вычислений лучше формулировать иначе: отклоняется альтернативная гипотеза H1: a > 10 .
Важно помнить, что гипотеза проверялась в предположении о нормальности выборки.
Пример 5
Пример 5. Задана выборка, содержащая 150 значений случайной величины, о которой известно, что она распределена нормальное, её математическое ожидание Mx = a неизвестно, но известна дисперсия Dx = s2 = 0.1.
Задача состоит в проверке с уровнем значимости 
гипотезы H0: a = 10 при односторонней альтернативной гипотезе H1: a < 10.
На приведенном ниже рисунке приведен фрагмент листа Excel с решением задачи.
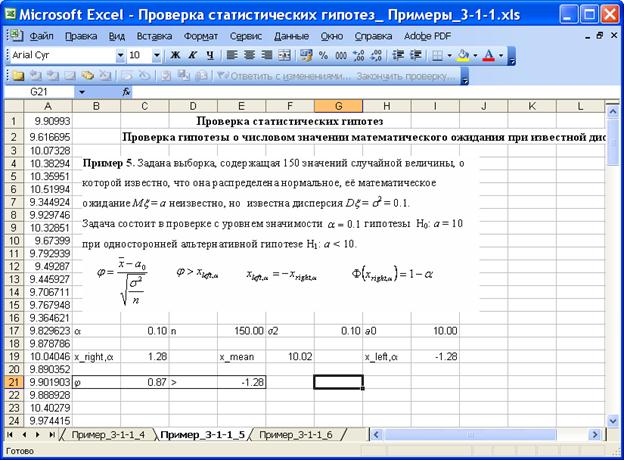
Значение критерия j = 0.87, область принятия нулевой гипотезы (– ¥, 1.28), значение критерия попадает в область принятия нулевой гипотезы, 0.87<1.28, нулевая гипотеза H0: a = 10 принимается с уровнем значимости 0.1.
Важно помнить, что гипотеза проверялась в предположении о нормальности выборки.
Пример 6
Пример 6. Задана выборка, содержащая 150 значений случайной величины, о которой известно, что она распределена нормальное, её математическое ожидание Mx = a неизвестно, но известна дисперсия Dx = s2 = 0.1.
Задача состоит в проверке с уровнем значимости 
гипотезы H0: a = 10 при односторонней альтернативной гипотезе H1: a > 10.
На приведенном ниже рисунке приведен фрагмент листа Excel с решением задачи.
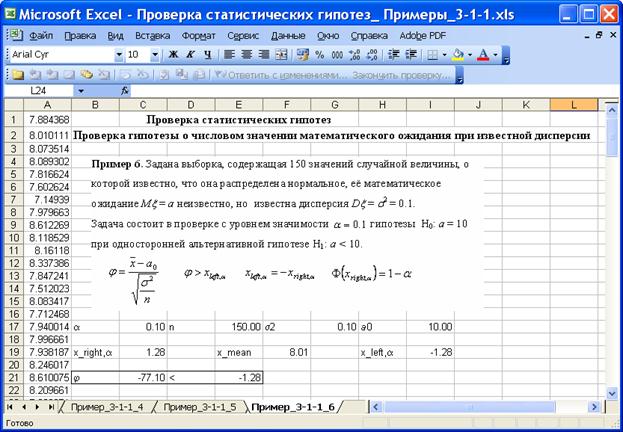
Значение критерия j = – 77.10, критическая область ( –¥, –1.28), значение критерия попадает в критическую область– 77.10<–1.28, нулевая гипотеза H0: a = 10 отклоняется с уровнем значимости 0.1, принимается альтернативная гипотеза H1: a < 10 .
Важно помнить, что гипотеза проверялась в предположении о нормальности выборки.
