Парная корреляция
Для измерения тесноты статистической связи между случайными величинами ![]() и
и ![]() введён коэффициент корреляции
введён коэффициент корреляции ![]() , который можно вычислить, если известна функция распределения системы из двух случайных величин (совместная функция распределения).
, который можно вычислить, если известна функция распределения системы из двух случайных величин (совместная функция распределения).
Поскольку на практике истинная совместная функция корреляции ![]() неизвестна, задача состоит не в вычислении, а в получении оценки коэффициента корреляции по результатам эксперимента, по выборке.
неизвестна, задача состоит не в вычислении, а в получении оценки коэффициента корреляции по результатам эксперимента, по выборке.
Получив оценку, следует ответить на вопрос «значимо ли оцененный коэффициент корреляции отличен от нуля», и если это отличие значимо, то для формулировки содержательного и точного утверждения о присутствии или отсутствии статистической связи между случайными величинами, следует построить доверительный интервал для коэффициента корреляции.
Итак, для исследования тесноты стохастической связи случайных величин ![]() и
и ![]() в нашем распоряжении выборка значений случайных величин, полученная в серии из
в нашем распоряжении выборка значений случайных величин, полученная в серии из ![]() одинаковых экспериментов:
одинаковых экспериментов:
Номер эксперимента |
Значения |
Значения |
1 |
|
|
2 |
|
|
… |
… |
… |
|
|
|
Выборочный коэффициент корреляции (точечная оценка коэффициента корреляции) вычисляется по формуле
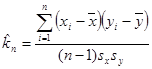 ,
,
где, как обычно, ![]() ,
, ![]() – выборочные средние,
– выборочные средние, ![]() ,
, ![]() – стандартные отклонения, квадратные корни из выборочных дисперсий.
– стандартные отклонения, квадратные корни из выборочных дисперсий.
Когда оценка ![]() получена, проверяем значимость коэффициента корреляции.
получена, проверяем значимость коэффициента корреляции.
Формулируем нулевую гипотезу ![]() против альтернативы
против альтернативы ![]() .
.
Если известно, что двумерный вектор ![]() , система случайных величин
, система случайных величин ![]() и
и ![]() , распределён по двумерному нормальному закону, то критерием для проверки гипотезы служит «агрегат»
, распределён по двумерному нормальному закону, то критерием для проверки гипотезы служит «агрегат»
 .
.
Этот «агрегат», эта случайная величина, в предположении о справедливости нулевой гипотезы, имеет распределение Стьюдента с ![]() -мя степенями свободы.
-мя степенями свободы.
Зададимся уровнем значимости ![]() и вычислим критическую точку
и вычислим критическую точку ![]() , решение уравнения
, решение уравнения ![]() .
.
Если ![]() , то событие
, то событие ![]() представляется вполне возможным, с уровнем значимости
представляется вполне возможным, с уровнем значимости ![]() не отвергаем гипотезу
не отвергаем гипотезу ![]() о нулевом значении коэффициента корреляции. Коэффициент корреляции полагаем незначимым. Полагаем, что никакой статистической связи между случайными величинами
о нулевом значении коэффициента корреляции. Коэффициент корреляции полагаем незначимым. Полагаем, что никакой статистической связи между случайными величинами ![]() и
и ![]() нет.
нет.
Если же ![]() , то событие
, то событие ![]() маловероятно, отвергаем с уровнем значимости
маловероятно, отвергаем с уровнем значимости ![]() гипотезу
гипотезу ![]() о нулевом значении коэффициента корреляции, принимаем альтернативу,
о нулевом значении коэффициента корреляции, принимаем альтернативу, ![]() . Коэффициент корреляции полагаем значимым. Допускаем существование статистической связи между случайными величинами
. Коэффициент корреляции полагаем значимым. Допускаем существование статистической связи между случайными величинами ![]() и
и ![]() . Переходим к построению доверительного интервала для коэффициента корреляции.
. Переходим к построению доверительного интервала для коэффициента корреляции.
Воспользуемся методикой Фишера. Он показал, что при ![]() величина
величина ![]()
распределена практически нормально с математическим ожиданием ![]() и дисперсией
и дисперсией ![]() .
.
Тогда, если ![]() , доверительная вероятность, а точки
, доверительная вероятность, а точки ![]() – границы критической двусторонней области для стандартного нормального распределения, то доверительный интервал для случайной величины
– границы критической двусторонней области для стандартного нормального распределения, то доверительный интервал для случайной величины ![]() записывается в виде
записывается в виде ![]() , обозначим его
, обозначим его ![]() .
.
Отсюда, выполнив несложные алгебраические вычисления (решив систему неравенств), получим доверительный интервал для коэффициента корреляции ![]() :
:
![]() ,
,
где решения уравнений ![]() ,
, ![]() ,
, ![]() – тангенс гиперболический.
– тангенс гиперболический.
И тогда можно утверждать, что с доверительной вероятностью ![]() интервал
интервал ![]() накрывает истинное значение коэффициента корреляции
накрывает истинное значение коэффициента корреляции ![]() .
.
По величине значений границ этого интервала мы сможем формулировать утверждения относительно тесноты статистической связи между случайными величинами ![]() и
и ![]() . О том, что эта связь существует, мы утверждаем на основании проверенной нами значимости коэффициента корреляции.
. О том, что эта связь существует, мы утверждаем на основании проверенной нами значимости коэффициента корреляции.
Замечание. Исторически так сложилось, что гиперболические функции были не «в почете» у представителей гуманитарных наук и Фишер дал своё имя функции ![]() , которая есть не что иное, как обычный гиперболический арктангенс (ареатангенс). Компьютеров тогда не было и для практической работы были составлены таблицы функции Фишера и обратной. Разработчики Excel, следуя традиции, включили в число функций пакета одинаковые функции под разными именами, т.е. есть одинаковые функции ATANH и ФИШЕР, а также одинаковые функции TANH и ФИШЕРОБР
, которая есть не что иное, как обычный гиперболический арктангенс (ареатангенс). Компьютеров тогда не было и для практической работы были составлены таблицы функции Фишера и обратной. Разработчики Excel, следуя традиции, включили в число функций пакета одинаковые функции под разными именами, т.е. есть одинаковые функции ATANH и ФИШЕР, а также одинаковые функции TANH и ФИШЕРОБР
Пример 1
Пример 1.![]() Исследовать тесноту статистической связи между случайными величинами
Исследовать тесноту статистической связи между случайными величинами ![]() и
и ![]() , представленными выборочными значениями
, представленными выборочными значениями
|
|
37 |
39 |
33 |
40 |
15 |
35 |
36 |
48 |
26 |
53 |
24 |
42 |
15 |
54 |
33 |
54 |
44 |
50 |
34 |
53 |
63 |
46 |
8 |
50 |
44 |
43 |
43 |
55 |
31 |
51 |
На приведенном ниже рисунке изображён фрагмент листа Excel с вычислениями.
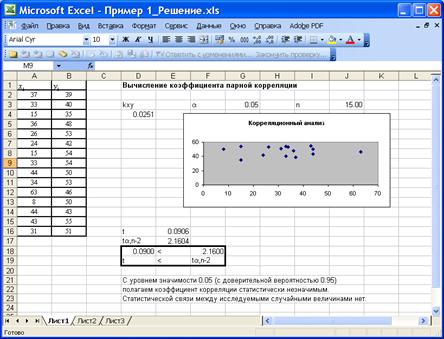
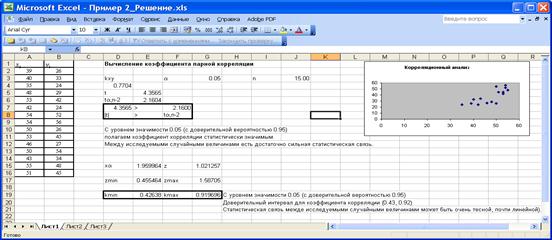
Пример 2
Пример 2.![]() Исследовать тесноту статистической связи между случайными величинами
Исследовать тесноту статистической связи между случайными величинами ![]() и
и ![]() , представленными выборочными значениями
, представленными выборочными значениями
|
|
39 |
26 |
40 |
33 |
35 |
24 |
48 |
29 |
53 |
42 |
42 |
24 |
54 |
52 |
54 |
56 |
50 |
26 |
53 |
45 |
46 |
27 |
50 |
54 |
43 |
34 |
55 |
48 |
51 |
45 |
На приведенном ниже рисунке изображён фрагмент листа Excel с вычислениями.