6. 0. Дисперсионный анализ. Обсуждение
Дисперсионным анализом называют статистический анализ результатов, зависящих от качественных факторов.
Дисперсионный анализ применяют для изучения влияния качественных признаков на количественную переменную.
Например. Владелец трёх магазинов, расположенных в трех разных местах, вынужден закрыть два из них. Как оставить? Необходимо определить, существует ли статистически значимое отличие между объемами реализации в магазинах. Если да, владелец оставит магазин с наибольшим среднесуточным объемом продаж. Если же разница объема реализации окажется статистически незначимой, то основанием для выбора должны быть другие показатели. Выяснить, влияет ли расположение магазина (качественный фактор) на объём продаж (количественная переменная) задача однофакторного дисперсионного анализа.
Другой пример. Политические взгляды граждан разделены на семь групп и упорядочены, от крайне либеральных до крайне консервативных.
Выяснить, есть ли значимое линейное увеличение среднего возраста граждан при рассмотрении групп, упорядоченных в направлении от либеральных до консервативных, – задача однофакторного дисперсионного анализа.
А вот пример задачи для двухфакторного анализа. На количество продаж товара, помимо размеров магазина, часто влияет расположение полок с товаром. Здесь два признака: размер магазина и расположение полок. При анализе конкретной ситуации может выясниться, например, что оба фактора влияют на объёмы продаж, но их взаимодействие значимым не является.
Обсудим модель с одним фактором. Пусть, например, ставится задача исследования влияния технологии обработки почвы (качественный фактор) на урожайность ( количественная переменная). Обозначим для удобства обсуждения конкретную технологию ![]()
![]() — уровнем фактора, m— число технологий;
— уровнем фактора, m— число технологий; ![]() — урожайность культуры, полученную в j-м году при использовании i -й технологии,
— урожайность культуры, полученную в j-м году при использовании i -й технологии, ![]() — число лет, в течение которых производились наблюдения за применением технологии
— число лет, в течение которых производились наблюдения за применением технологии ![]() . Данные удобно представить в таблице.
. Данные удобно представить в таблице.
|
1 |
2 |
3 |
... |
|
|
|
|
|
... |
|
|
|
|
|
... |
|
... |
... |
... |
... |
... |
... |
|
|
|
|
... |
|
Предполагается, что каждая случайная величина ![]() может быть представлена в виде
может быть представлена в виде ![]() ,
,
где ![]() — урожайность, характерная для технологии
— урожайность, характерная для технологии ![]() , а
, а ![]() — случайные величины, которые описывают суммарный вклад всех случайных факторов, влияющих на итоговую урожайность. Чаще всего полагают, что
— случайные величины, которые описывают суммарный вклад всех случайных факторов, влияющих на итоговую урожайность. Чаще всего полагают, что ![]() независимы, распределены нормально с нулевым математическим ожиданием и одинаковой дисперсией.
независимы, распределены нормально с нулевым математическим ожиданием и одинаковой дисперсией.
Задача, которую предстоит решить: влияет выбор технологии обработки почвы на урожайность культуры или нет.
На математическом языке это означает, что по результатам эксперимента необходимо проверить справедливость статистической гипотезы о том, что все технологии ![]() одинаково эффективны.
одинаково эффективны.
Анализ результатов будет основан на сопоставлении двух оценок неизвестной дисперсии случайных величин ![]() .
.
Одна из этих оценок не зависит от того, верна ли гипотеза. Для другой оценки это предположение существенно, т.е. эта оценка будет близка к значению дисперсии только тогда, когда гипотеза верна.
Если обе оценки близки, то гипотезу следует принять. Если же оценки существенно отличаются, то – отвергнуть.
Для оценки степени влияния фактора (технологии) используют выборочный коэффициент детерминации ![]() . Коэффициент детерминации
. Коэффициент детерминации ![]() показывает, какую часть в общей дисперсии величин
показывает, какую часть в общей дисперсии величин ![]() составляет часть, обусловленная зависимостью от фактора.
составляет часть, обусловленная зависимостью от фактора.
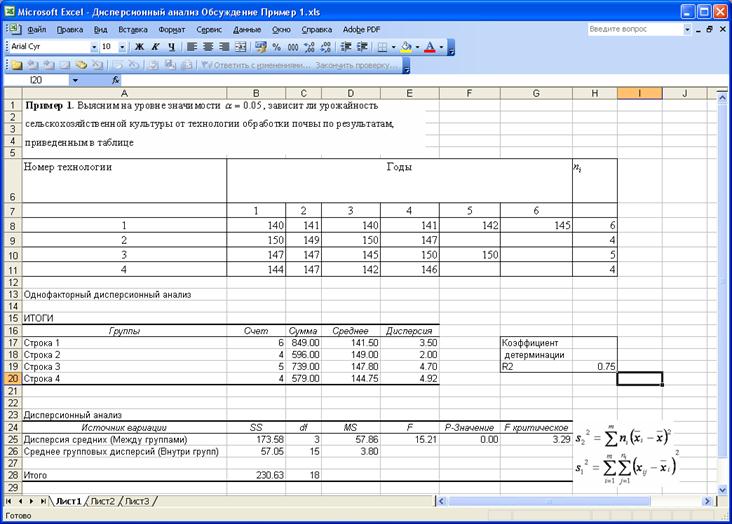
Пример
Выясним на уровне значимости ![]() , зависит ли урожайность сельскохозяйственной культуры от технологии обработки почвы по результатам, приведенным в таблице
, зависит ли урожайность сельскохозяйственной культуры от технологии обработки почвы по результатам, приведенным в таблице
Номер технологии |
Годы |
|
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
140 |
141 |
140 |
141 |
142 |
145 |
6 |
2 |
150 |
149 |
150 |
147 |
|
|
4 |
3 |
147 |
147 |
145 |
150 |
150 |
|
5 |
4 |
144 |
147 |
142 |
146 |
|
|
4 |
На приведенном ниже рисунке изображён фрагмент листа Excel, содержащий вычисления.