Инструменты Excel для вычисления числовых характеристик выборки
Процедура «Описательные статистики » пакета «Анализ данных.
В процедуре автоматически вычисляются следующие числовые характеристики выборки:
- среднее –
; - стандартная ошибка среднего –
; - медиана – решение уравнения
, где 
– эмпирическая функция распределения; - мода – чаще всего встречающееся в выборке значение;
- выборочная дисперсия –
; - стандартное отклонение –
; - эксцесс –
; - коэффициент асимметрии –
; - размах варьирования –
; - наибольшее значение –
; - наименьшее значение –
; - объём выборки –
.
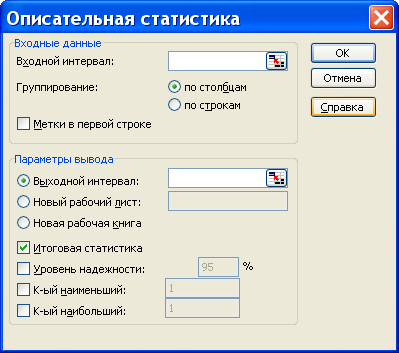
Для того чтобы выполнить вычисления, вводим в поле «Водной интервал» адреса ячеек, в которых записаны выборочные значения;
помечаем «Выходной интервал» и вводим в поле адрес первой ячейки, начиная с которой в листе Excel будет отображён резгультат; помечаем «Итоговая статистика»:
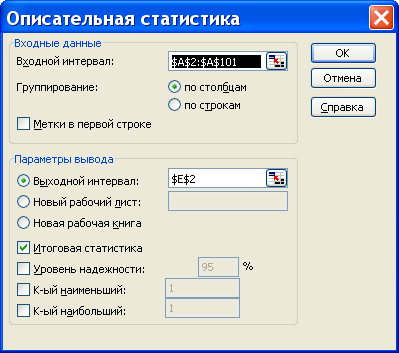
Результаты вычислений процедуры представлены в виде таблицы:
Столбец1 |
|
|
|
Среднее |
120.10 |
Стандартная ошибка |
0.22 |
Медиана |
120.12 |
Мода |
118.69 |
Стандартное отклонение |
2.15 |
Дисперсия выборки |
4.63 |
Эксцесс |
0.21 |
Асимметричность |
-0.16 |
Интервал |
11.21 |
Минимум |
114.46 |
Максимум |
125.67 |
Сумма |
12010.34 |
Счет |
100 |
Здесь: «Асимметричность» – коэффициент асимметрии, «Интервал» – размах варьирования, «Счёт» – объём выборки.
Функция «Квартиль» для вычисления квартилей и межквартильного размаха
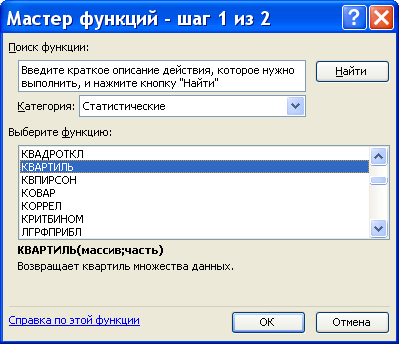
КВАРТИЛЬ(массив;часть)
Функция вычисляет (в зависимости от значения параметра «Часть»), выборочные значения верхней квартили («Часть» = 3) или нижней квартили («Часть» = 13), медиану («Часть» = 2) , наибольшее («Часть» = 4) или наименьшее («Часть» = 03) значения для выборки, определённой как «массив»..
- верхняя квартиль – решение уравнения
, где 
– эмпирическая функция распределения; - нижняя квартиль – решение уравнения
; - медиана – решение уравнения
.
