Вероятностное пространство

Центральным понятием теории вероятности является понятие вероятностного пространства.

Начнем с пространства элементарных событий. Так называется перечень, список, реестр или, как говорят математики, множество событий, которым может закончиться случайный эксперимент.

Поясним сказанное примерами.

Случайный эксперимент – бросание монеты. Чаще всего говорят, что этот эксперимент заканчивается одним из двух событий – выпадает «орёл» или «решка». Хотя некоторые говорят, что этот перечень неполный – не хватает события «монета упала на ребро». Кто прав? И одни и другие! Всё зависит от задачи, которую предстоит решить. Конечно, «падение на ребро» - крайне маловероятное событие и чаще всего такой исход эксперимента можно не принимать во внимание. Итак, будем считать, что в этом эксперименте возможны только два взаимоисключающие исхода , два события, и поэтому пространство элементарных событий состоит из двух элементов –

В этой записи буквой  обозначено пространство элементарных событий, а буквы О и Р обозначают сами события.

Ещё один пример случайного эксперимента – бросание игральной кости. Здесь пространство элементарных событий состоит из 6 элементов

Цифрой 1 обозначено событие, состоящее в том, что в результате эксперимента выпала грань, на которой изображена одна точка, 2 – две точки и т.д.

Здесь важно понять,  что имеется в виду, когда говорят об элементарных событиях. Вспомним событие, которое состоит в том, что на кости выпадет четное число очков. Легко догадаться, что в нашей модели оно не элементарное – состоит из трёх элементарных.

В теории вероятности подразумевается, что пространство элементарных событий состоит из действительно элементарных событий. Описание элементарных событий – первая задача  исследователя.

В дальнейшем будем считать, что пространство элементарных событий построено и имеет вид

где - элементарные события,  – число возможных исходов эксперимента.

Для простоты будем считать, что число возможных исходов конечно.

В теории вероятностей этот случай называется дискретной схемой.

Итак, со случайным экспериментом мы, в первую очередь, связываем пространство элементарных событий.

Построение пространства элементарных событий, чаще всего,  очень несложная процедура, хотя по числу элементов пространство может оказаться весьма громоздким. Вот несколько примеров.

В популярной лотерее 7 из 49 пространство элементарных событий содержит более чем  143 миллиона элементов.

Случайный эксперимент состоит в бросании двух игральных костей. Пространство элементарных событий для этого эксперимента можно изобразить в виде

 

Конечно это не матрица. Можно было перечислить все элементарные события, записав их в строчку и в любом порядке. Но так удобнее! Кстати, об обозначениях: элемент (3,5) соответствует элементарному событию – на первой кости выпало 3 очка, на второй – 5 очков.

            От элементарных событий перейдём к событиям.

Событие – это любое подмножество пространства элементарных событий.

 

В эксперименте с бросанием игральной кости пространство элементарных событий
.

Существует 2⁶ = 64 различных подмножеств множества ,  64 различных события, которыми может закончиться такой эксперимент:

Событие А – выпало нечётное число очков состоит из трёх элементарных событий, А ={1, 3, 5}, событие А происходит, если эксперимент заканчивается  одним из тех элементарных событий, которые входят в событие А;

событие В – выпало число очков делится на 3 без остатка, B = {3,6}.

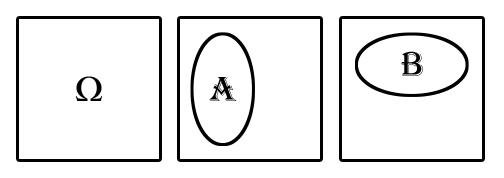
Важно понимать и помнить, что эксперимент всегда заканчивается одним и только одним элементарным событием.

Всё пространство элементарных событий  называется достоверным событием.

Каждому событию можно поставить в соответствие противоположное событие .

Противоположное событие к событию – событие .

Противоположное событие к событию B = {3,6} – событие .

Противоположное событие к событию   не содержит элементарных событий – невозможное событие, его обозначают .

 

       

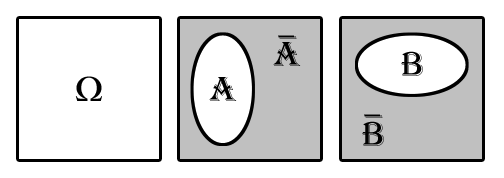
 В число событий входят:

все элементарные события;

всё пространство элементарных событий ;

 противоположное   событие .

            События можно складывать и перемножать.

Суммой двух событий А и В называется событие А+В, в котором присутствуют все элементарные события из А и все элементарные события из В.

Сумма А+В ={2, 4, 6} + {3, 6} = {2, 3, 4, 6}. Действительно в сумме  А+В присутствуют все элементарные события из А и все элементарные события из В.

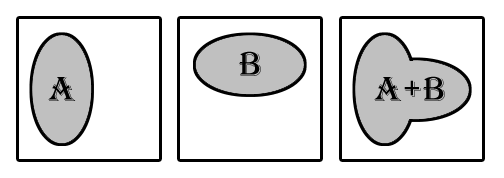
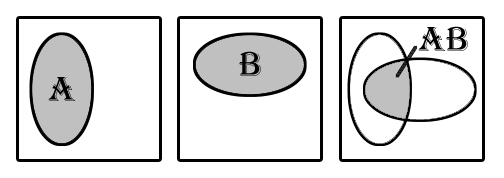
Произведением А·В  событий А и В (обозначается А·В ) называется событие, которое состоит из тех и только тех элементарных, которые входят одновременно и в А и в В.

В последнем примере  А·В = ={2, 4, 6} · {3, 6} = {6}, число очков чётное и делится на 3 без остатка.

 

Для «построения» теории вероятностей у нас уже есть:

пространство элементарных событий;

 события (состоящие из элементарных);

простейшие операции над событиями, сложение, умножение, дополнение.

Теперь каждому элементарному событию  из пространства элементарных событий  припишем положительное число  так, что все  и

Числа  называются вероятностями элементарных событий.

Сумма вероятностей всех элементарных событий равна 1.

Основная формула теории вероятностей на этом этапе выглядит так

Это означает, что вероятность P(A) любого события А равна сумме вероятностей входящих в него элементарных событий.

По идейной нагрузке, которую несёт эта формула, она ничем не отличается от такой: масса любого агрегата равна сумме масс составляющих его деталей.

По этой формуле сразу получаем , P(Æ) = 0.

Практически очевидно, что , .  

Если в событиях А и В нет одинаковых элементарных событий, то

Если же такие события есть, то события A и B называются совместными событиями, и при подсчёте они войдут в итоговую сумму дважды.

Чтобы избежать этой ошибки исключим повторное суммирование. Теперь формула примет следующий вид

Если  события A и B называются несовместными событиями, то новая формула вероятности суммы событий совпадает с предыдущей формулой.

Лучше всегда пользоваться формулой