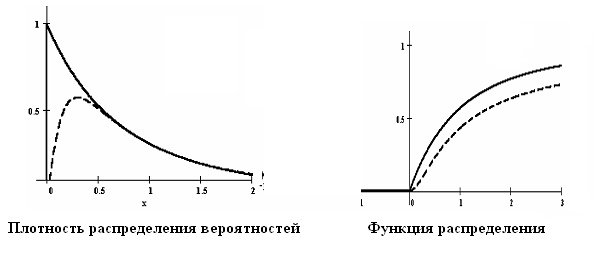
Нормальное распределение и производные от него
Нормальное распределение играет исключительно важную роль в теории вероятностей и математической статистике.
Случайная величина 
нормально распределена с параметрами 
и 
, 
, если ее плотность распределения имеет вид:
.
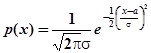Если случайная величина 
имеет нормальное распределение с параметрами 
и 
, то обычно пишут 
.
Случайная величина 
имеет стандартное нормальное распределение, если 
и 
, 
. Плотность стандартного нормального распределения имеет вид
,
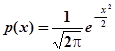а функция распределения стандартной нормальной величины
,
где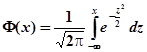 
— функция Лапласа.
Функция распределения нормальной величины 
также выражается через функцию Лапласа:
.
- Ниже приведены графики плотности вероятностей и функций распределения для
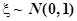и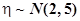 
.
- Распределение хи-квадрат (
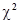- распределение) - Пусть
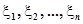— независимые случайные величины, каждая из которых имеет стандартное нормальное распределение 
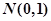. Составим случайную величину 
.- Ее закон распределения называется
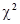- распределением с 
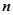степенями свободы. Для справочных целей приведем здесь выражение плотности распределения этой случайной величины: 
- где
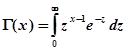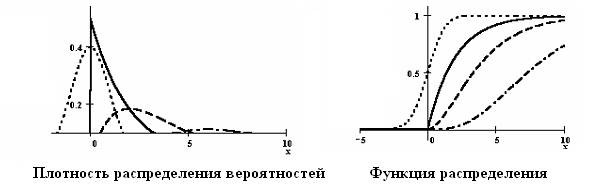
— гамма-функция Эйлера. - Ниже приведены графики плотности вероятностей и функций распределения для
-распределения с двумя, четырьмя и восемью степенями свободы,. Для сравнения приведены графики для 
.
Распределение Стьюдента
Пусть случайная величина 
имеет стандартное нормальное распределение, а случайная величина 
— 
-распределение с 
степенями свободы. Если 
и 
— независимы, то про случайную величину 
говорят, что она имеет распределение Стьюдента с числом степеней свободы 
; доказано, что плотность вероятности этой случайной величины вычисляется по формуле:
, 
.
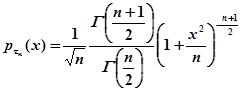При больших 
распределение Стьюдента практически не отличается от 
.
- Ниже приведены графики плотности вероятностей и функций распределения для
. Для сравнения приведены графики для 
.
F-распределение Фишера
Пусть случайные величины 
и 
независимы и имеют распределение 
с 
и 
степенями свободы соответственно. Тогда случайная величина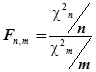 
имеет F-распределение с плотностью вероятности
, 
.
Ниже приведены графики плотности вероятностей и функций распределения для 
и 
.
