Основные распределения и их свойства
Подобно тому, как в планиметрии изучают не произвольные, а вполне конкретные, базовые, геометрические фигуры: треугольник, прямоугольник, окружность, и т.п., в прикладной статистике столь же популярны нормальное распределение и производные от него: распределение 
, Стьюдента и Фишера.
В справочных целях ниже приведены формулы для математических ожиданий, дисперсий и плотностей вероятностей наиболее известных стандартных распределений:
биномиальное распределение: 
, 
, 
;
геометрическое распределение: 
, 
, 
;
гипергеометрическое распределение: 
, 
, 
;
- пуассоновское распределение:
, 
, 
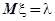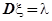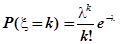; - pавномерное распределение:
, 
, 
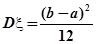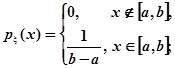; - экспоненциальное (показательное) распределение:
, 
, 
;
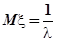нормальное распределение 
: 
, 
, 
;
распределение хи-квадрат (
- распределение) с 
степенями свободы: 
,
, 
где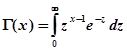 
— гамма-функция Эйлера;
распределение Стьюдента с 
степенями свободы, 
: 
, 
, 
;
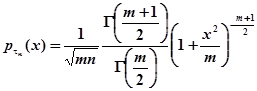F-распределение Фишера с 
и 
степенями свободы: 
, 
, 
, 
;
распределение Парето имеет математическое ожидание только при 
, а дисперсию при 
: распределение Парето: 
, 
;
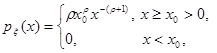
логистическое распределение: 
, 
, 
.
