Эмпирические распределения. Гистограммы. Полигоны частот

Гистограмма
Первичная обработка выборочных данных состоит обычно в отыскании максимального — xmax и минимального xmin значений выборки, а также размаха варьирования R = xmax – xmin.
Следующий этап первичной обработки выборки — группировка и ее графическое представление. Группировка выборки объема n состоит в следующем. Промежуток [xmin, xmax] разбивают на m интервалов группировки (чаще всего одинаковой длины и обычно 7£ m £20) и подсчитывают количество nj  выборочных значений, которые попали в j-й интервал. Каждый интервал группировки Dj = (aj, bj) представлен своими левой aj и правой bj границами и числом nj элементов выборки, ему принадлежащих. Удобнее каждый интервал представлять не двумя границами, а одним числом — срединным значением.
Наиболее наглядная форма графического представления группировки — гистограмма.
Если d1, d2, …, dm — длины интервалов группировки, hj = nj /n — относительные частоты попадания наблюдений в  j-й интервал группировки, а ¾
— их середины,  то можно построить график ступенчатой функции 
, , .
Этот график называется гистограммой.
Очевидно, что величина интервала группировки существенно влияет на вид гистограммы. При малой их ширине в каждый интервал попадает незначительное число наблюдений, или даже не попадает ни одного, гистограмма становится сильно «изрезанной» и плохо передает основные особенности изучаемого распределения.
Несколько общих правил:

• Перед началом группировки упорядочить выборочные значения по возрастанию (такая, упорядоченная по возрастанию выборка называется вариационным рядом).
• При выборе числа интервалов группировки ориентироваться на 10-20 интервалов.
• Использовать не перекрывающиеся открытые интервалы одинаковой длины, охватывающие всю область данных.

Пример 1

Видео

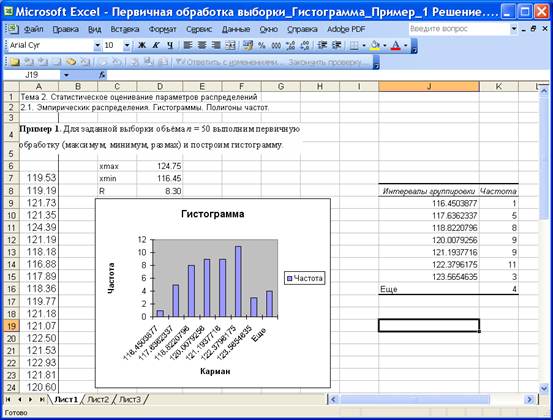
Пример 1. Для заданной выборки объёма n = 50 выполним первичную обработку (максимум, минимум, размах) и построим гистограмму.

На приведенном ниже рисунке изображён фрагмент листа Excel с выборочными значениями и результатами первичной обработки выборки.

Полигоны частот

Другая форма графического представления группированных данных — полигон частот.

Полигон частот — это ломаная линия, соединяющая точки с координатами , т.е. точек с абсциссами, равными серединам интервалов группировки и ординатами, равными соответствующим частотам.

Можно также построить полигон накопленных частот — график ломаной, соединяющей точки с координатами  или  — точек с абсциссами, равными правым границам интервалов группировки и ординатами, равными соответствующим накопленным частотам или относительным накопленным частотам.

Пример 2

Видео

Пример 2. Для заданной выборки объёма n = 50 построим полигон частот и полигон накопленных частот.

На приведенном ниже рисунке изображён фрагмент листа Excel с выборочными значениями и графиками – полигоном частот и полигоном накопленных частот.