Проверка гипотезы о числовом значении дисперсии нормально распределённой случайной величины
Пусть x — нормально распределенная случайная величина с неизвестной дисперсией Dx = s2, представленная выборочными значениями
x1, x2, …, xn.
Задача состоит в проверке гипотезы о том, что неизвестный параметр s2 равен заданному числу.
Пусть дана некоторая оценка 
неизвестной дисперсии 
, построенная по выборке
x1, x2, …, xn.
Предположим, что истинное значение дисперсии равно 
.
Поскольку оценка 
— случайная величина, то выборочное значение 
, вряд ли будет совпадать с 
. В связи с этим возникает вопрос: при каком отклонении 
от 
и с какой степенью уверенности можно утверждать, что истинное значение дисперсии 
отлично от 
? Ответом на этот вопрос может быть значение вероятности того, что величина 
, вычисленная в предположении, что 
, больше некоторого фиксированного числа.
Если эта вероятность мала, то мы являемся свидетелями маловероятного события, т.е. отличие эмпирического значения 
от гипотетического значения 
представляется значимым и гипотеза о том, что 
должна быть отвергнута.
Если же эта вероятность велика, то отклонение 
от 
, по-видимому, обусловлено естественной случайностью, и гипотеза 
может быть принята.
Сформулируем нулевую гипотезу о том, что дисперсия нормального распределения s2 равна заранее заданному числу s02 — H0:s2 = s02.
В процедуре проверки гипотезы будет использован критерий
, где 
и 
— несмещенные точечные оценки дисперсии и математического ожидания.
Критерий j имеет распределение c2 с (n-1) степенями свободы.
Рассмотрим три случая альтернативных гипотез:
- H1: s2 ¹ s 02;
- H1: s2 > s02;
- H1: s2 < s02.
В первом из этих случаев, двусторонняя альтернатива H1:s2 ¹ s02, критическая область двусторонняя и ее границы определяются из условий 
и 
.
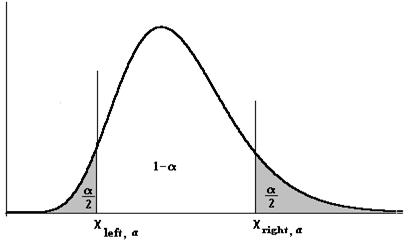
Критическая область для альтернативной гипотезы H1:s2¹s02
Зададимся некоторым уровнем значимости a и найдем значение 
и 
уравнения как решения уравнений
и 
,
где 
— функция распределения c2 с (n –1) степенями свободы.
Когда критическая область найдена, можно по выборке вычислить значение критерия j и проверить попадает ли это значение в критическую область или в область принятия гипотезы.
Если
или
, значение критерия попало в критическую область, гипотеза H0 отвергается, принимается гипотеза альтернативная гипотеза H1.
Если же 
, значение критерия попало в область принятия гипотезы, принимается гипотеза H0, альтернативная гипотеза H1 отклоняется.
Если гипотеза H0:s2 = s02 проверяется против правосторонней альтернативыH1:s2>s02 , то критическая область (область отклонения гипотезы H0) правостороння; при заданном уровне значимости a она представляет собой интервал 
, граница которого 
удовлетворяет условию 
и находится как решение уравнения 
, где 
— функция распределения c2 с (n-1) степенями свободы.
Если гипотеза H0:s2=s02 проверяется против левосторонней альтернативыH1:s2 < s02 , то критическая область левосторонняя; при заданном уровне значимости a она представляет собой интервал 
, граница которого 
удовлетворяет условию 
и находится как решение уравнения 
, где 
— функция распределения c2 с (n-1) степенями свободы.
Пример 1
Пример 1. Задана выборка, содержащая 150 значений случайной величины, о которой известно, что она распределена нормально.
Задача состоит в проверке с уровнем значимости 
гипотезы H0: s2 = 0.1 для трёх альтернативных гипотез H1:s2 ¹ 0.1, H1s2 > 0.1 и H1:s2 < 0.1.
Внимание! В Excel функция распределения случайной величины определена нестандартно: Fx(x) = P(x > x). Поэтому для вычисления квантиля c2left, n вводим в качестве аргумента функции ХИ2ОБР значение вероятности, равное 
.
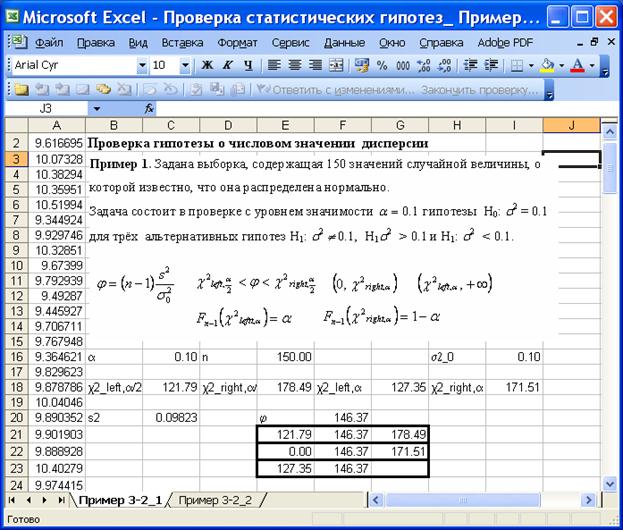
Значение критерия j = 146.37. Область принятия гипотезы H0: s2 = 0.1 против двусторонней альтернативы H1: s2 ¹ 0.1 — промежуток (121.79, 178.49). Значение критерия попадает в область принятия нулевой гипотезы, 121.79 < 146.37 < 178.49, нулевая гипотеза H0: s2 = 0.1 против альтернативы H1: s2 ¹ 0.1 принимается с уровнем значимости 0.1.
Область принятия гипотезы H0: s2 = 0.1 против правосторонней альтернативы H1: s2 > 0.1 — промежуток (0, 178.49). Значение критерия попадает в критическую область, 0< 146.37 <178.49, нулевая гипотеза H0: s2 = 0.1 против альтернативы H1: s2 > 0.1 принимаетсяс уровнем значимости 0.1.
Область принятия гипотезы H0: s2 = 0.1 против левосторонней альтернативы H1: s2 < 0.1 — промежуток (121.79, +¥). Значение критерия попадает в область принятия нулевой гипотезы, 121.79 < 146.37, нулевая гипотеза H0: s2 = 0.1 против альтернативы H1: s2 < 0.1 принимается с уровнем значимости 0.1.
Важно помнить, что гипотеза проверялась в предположении о нормальности выборки.
Пример 2
Пример 2. Задана выборка, содержащая 150 значений случайной величины, о которой известно, что она распределена нормально.
Задача состоит в проверке с уровнем значимости 
гипотезы H0: s2 = 0.1 для трёх альтернативных гипотез H1:s2 ¹ 0.1, H1s2 > 0.1 и H1:s2 < 0.1.
На приведенном ниже рисунке изображён фрагмент листа Excel с решением задачи.
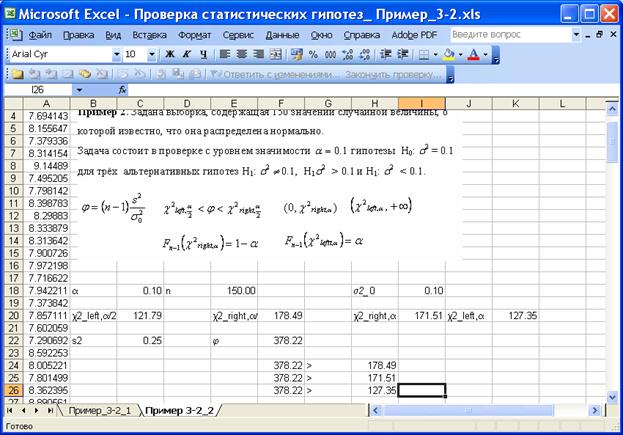
Значение критерия j = 378.22.
Область принятия гипотезы H0: s2 = 0.1 против двусторонней альтернативы H1: s2 ¹ 0.1 — промежуток (121.79, 178.49).
Значение критерия попадает в критическую область, 378.22 >178.49, с уровнем значимости 0.1 нулевая гипотеза H0:s2=0.1 отклоняется, принимается альтернатива H1: s2 ¹ 0.1.
Область принятия гипотезы H0: s2 = 0.1 против правосторонней альтернативы H1: s2 > 0.1 — промежуток (0, 178.49). Значение критерия попадает в критическую область, 378.22 >178.49, с уровнем значимости 0.1 нулевая гипотеза H0: s2 = 0.1 отклоняется, принимается альтернатива H1: s2 > 0.1.
Область принятия гипотезы H0: s2 = 0.1 против левосторонней альтернативы H1: s2 < 0.1 — промежуток (121.79, +¥). Значение критерия попадает в область принятия нулевой гипотезы, 121.79< 378.22, с уровнем значимости 0.1 принимается нулевая гипотеза H0: s2 = 0.1 против альтернативы H1: s2 < 0.1.
Поскольку известна точечная оценка дисперсии, s2 = 0.25, результат проверки нулевой гипотезы против альтернативы H1: s2 < 0.1 естественно сформулировать иначе: гипотеза H1: s2 < 0.1 не принимается с уровнем значимости 0.1.
Важно помнить, что гипотеза проверялась в предположении о нормальности выборки.
