Проверка гипотезы о равенстве математических ожиданий нормально распределённых случайных величин
Проверка гипотезы о равенстве математических ожиданий двух нормальных распределений c равными известными дисперсиями
Пусть x и h — независимые нормально распределенные случайные величины, представленные выборочными значениями соответственно
x1, x2, …, xn и y1, y 2, …, y m .
Задача состоит в проверке гипотезы о том, что равны неизвестные математические ожидания Mx = ax и Mh = ah. Значения дисперсий Dx = sx2 и Dh = sh2 известны.
Рассмотренная задача чрезвычайно важна в приложениях.
Например, на двух предприятиях производятся одинаковые товары и среднее значение некоторого параметра в контрольной партии с одного предприятия отличается от значения того же параметра, полученного при обследовании второго предприятия.
Возникает вопрос: эти различия статистически значимы или нет?
Различия обусловлены только случайными факторами, или различием в организации производства на предприятиях?
Итак, проверяем гипотезу ![]() против альтернативы
против альтернативы ![]() .
.
Если гипотеза ![]() верна, то величина
верна, то величина
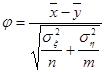
подчинена стандартному нормальному распределению ![]() .
.
Здесь ![]() ,
, ![]() и
и ![]() .
.
Известны статистические свойства этих случайных величин:
 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 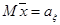 и
и  ;
;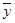 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами  и
и 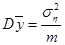 ;
;-
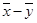 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами  и
и  .
.
Зададимся некоторым уровнем значимости ![]() . Границы критической области определяются из условий
. Границы критической области определяются из условий 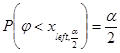 и
и ![]() ,
, ![]() — решение уравнения
— решение уравнения  , где
, где ![]() — функция распределения стандартного нормального распределения.
— функция распределения стандартного нормального распределения.
Когда критическая область найдена, можно вычислить по выборке значение критерия ![]() и проверить попадает ли оно в критическую область.
и проверить попадает ли оно в критическую область.
Если![]() или
или ![]() , то гипотеза
, то гипотеза ![]() о равенстве математических ожиданий отвергается, принимается альтернатива
о равенстве математических ожиданий отвергается, принимается альтернатива ![]() .
.
Если же ![]() , то принимается гипотеза
, то принимается гипотеза ![]() .
.
Пример 1
Пример 1. Заданы две выборки, содержащие соответственно 20 и 15 значений двух независимых случайных величин x и h, о которых известно, что они распределены нормально с известными дисперсиями Dx = sx2 = 2 и Dh = sh2= 3. Математические ожидания Mx = ax и Mh = ah неизвестны.
Задача состоит в проверке с уровнем значимости ![]() гипотезы H0: ax = ah против альтернативы H1:ax ¹ ah.
гипотезы H0: ax = ah против альтернативы H1:ax ¹ ah.
На приведенном ниже рисунке изображён фрагмент листа Excel с решением задачи.
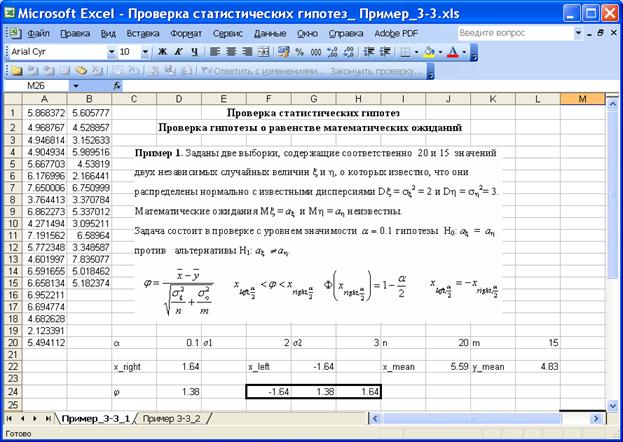
Значение критерия j = 1.38.
Область принятия гипотезы H0: ax = ah против двусторонней альтернативы H1: ax ¹ ah.— промежуток (–1.64, 1.64). Значение критерия попадает в критическую область, область отклонения нулевой гипотезы, -1.64 < 1.38 < 1.64, нулевая гипотеза H0: ax = ah против альтернативы H1:ax ¹ ah принимается с уровнем значимости 0.1, с вероятностью 0.90 математические ожидания случайных величин x и h равны между собой.
Проверка гипотезы о равенстве математических ожиданий двух нормальных распределений c равными, но неизвестными дисперсиями
Пусть x и h — независимые нормально распределенные случайные величины, представленные выборочными значениями соответственно
x1, x2, …, xn и y1, y 2, …, y m .
Задача состоит в проверке гипотезы о том, что равны неизвестные математические ожидания Mx = ax и Mh = ah. Значения дисперсий Dx = sx2 и Dh = sh2 равны между собой, sx2 = sh2=s2.
Итак, проверяем гипотезу ![]() против альтернативы
против альтернативы ![]() .
.
Если гипотеза ![]() верна, то величина
верна, то величина
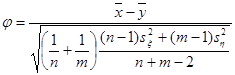
имеет распределение Стьюдента с ![]() степенями свободы
степенями свободы
Здесь ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Зададимся уровнем значимости ![]() и построим критическую область для альтернативной гипотезы
и построим критическую область для альтернативной гипотезы ![]() , которая в этом случае двусторонняя. Значение
, которая в этом случае двусторонняя. Значение ![]() находим как решение уравнения
находим как решение уравнения  , а
, а ![]() — решение уравнения
— решение уравнения 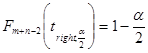 , где
, где ![]() — функция распределения Стьюдента с
— функция распределения Стьюдента с ![]() степенями свободы.
степенями свободы.
Когда критическая область найдена, можно вычислить по выборке значение критерия ![]() и проверить попадает ли оно в критическую область. Если
и проверить попадает ли оно в критическую область. Если![]() или
или![]() , то гипотеза
, то гипотеза ![]() отвергается и принимается гипотеза
отвергается и принимается гипотеза![]() .
.
Если же ![]() , то принимается гипотеза
, то принимается гипотеза ![]() .
.
Пример 2
Пример 2. Заданы две выборки, содержащие соответственно 20 и 15 значений двух независимых случайных величин x и h, о которых известно, что они распределены нормально с равными, но неизвестными дисперсиями Dx = Dh = s2.
Математические ожидания Mx = ax и Mh = ah неизвестны.
Задача состоит в проверке с уровнем значимости ![]() гипотезы H0: ax = ah против альтернативы H1:ax ¹ ah.
гипотезы H0: ax = ah против альтернативы H1:ax ¹ ah.
На приведенном ниже рисунке изображён фрагмент листа Excel с решением задачи.
Внимание!
Функция Excel СТЬЮДРАСПОБР(p, k) возвращает значение t, при котором
P(|x| > t) = p, x — значение случайной величины, имеющей распределение Стьюдента с k степенями свободы. Поэтому решение уравнения ![]() в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 1).
в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 1).
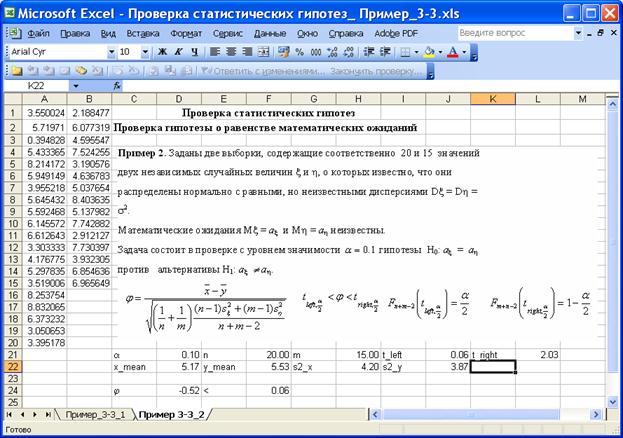
Значение критерия j = – 0.52. Область принятия гипотезы H0: ax = ah против двусторонней альтернативы H1: ax ¹ ah.— промежуток (0.06, 2.03). Значение критерия попадает в критическую область, –0.52< 0.06, нулевая гипотеза H0: ax = ah против альтернативы H1:ax ¹ ah отклоняется с уровнем значимости 0.1, с вероятностью 0.90 математические ожидания случайных величин x и h не равны между собой.