5. 1. Точечные оценки коэффициентов регрессии
В некотором эксперименте измерены значения пары случайных величин y и x
(x1, y1), (x2, y2), …(xn, yn).
Без ограничения общности можно считать, что величина x измерена точно, в то время как измерение величины y содержит случайные погрешности.
Это означает, что погрешность измерения величины x пренебрежимо мала по сравнению с погрешностью измерения величины y. Таким образом, результаты эксперимента можно рассматривать как выборочные значения случайной величины h(x), зависящей от x как от параметра.
Пусть требуется построить зависимость y(x).
Регрессией называют зависимость условного математического ожидания величины h(x) от x:
![]() .
.
Задача регрессионного анализа состоит в восстановлении функциональной зависимости y(x) по результатам измерений {(xi,yi)}, i = 1, 2, …, n.
Аппроксимируем искомую зависимость y(x) функцией f(x; a0, a1, …, ak).
Это означает, что результаты измерений можно представить в виде
![]() ,
,
где a0, a1, …, ak — неизвестные параметры регрессии, а ei — случайные величины, характеризующие погрешности эксперимента.
Обычно предполагается, что ei — это независимые нормально распределенные случайные величины с M(ei) = 0 и одинаковыми дисперсиями D(ei) = s2.
Параметры a0, a1, …, ak следует выбирать таким образом, чтобы отклонение значений предложенной функции от результатов эксперимента было минимальным. В качестве меры отклонения выберем величину
![]() ,
,
— параметры a0, a1, …, ak определим методом наименьших квадратов.
Рассмотрим простейший случай линейной регрессии.
Пусть выдвинута гипотеза о том, что функция f(x; a0, a1, …, ak) имеет вид
f(x; a, b)= ax + b.
Оценки параметров a и b находим из необходимого условия минимума функции ![]() :
:
приравняв нулю частные производные функции ![]() ,
,
![]() ,
,
получаем точечные оценки параметров (коэффициентов) регрессииa и b:
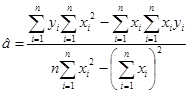 ,
, 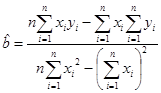 .
.
Здесь использованы принятые для точечных оценок обозначения ![]() .
.
Примеры
Пример 1
Пример 1. В таблице приведены некоторые экспериментальные данные:
x |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
y |
1.156 |
1.382 |
1.553 |
1.705 |
1.831 |
2.204 |
2.388 |
2.656 |
x |
0.9 |
1.0 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
|
y |
3.019 |
3.081 |
3.299 |
3.486 |
3.692 |
3.867 |
3.896 |
|
Будем искать зависимость y(x) в виде линейной функции y (x)= ax + b — найдём точечные оценки параметров (коэффициентов регрессии) a и b.
В Excel точечные оценки коэффициентов регрессии a и b можно вычислить одним из трёх способов: вычислением по формуле, использованием функции ЛИНЕЙН (возвращает значения a и b, вычисленные методом наименьших квадратов), используя процедуру «Регрессия» пакета «Анализ данных».
Первый способ — вычисление точечных оценок по формулам  . Ниже приведено изображение фрагмента листа Excel с решением задачи.
. Ниже приведено изображение фрагмента листа Excel с решением задачи.
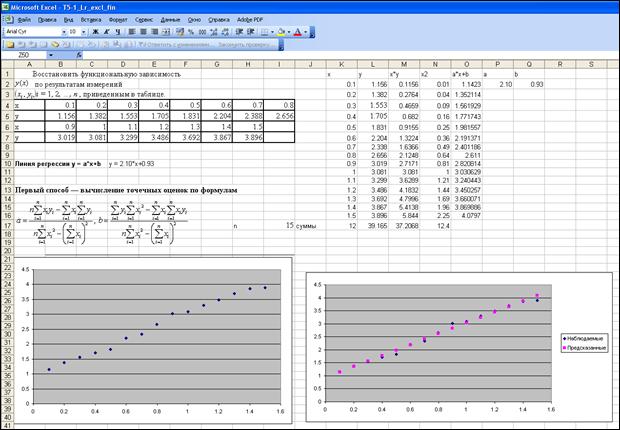
Получили a = 2.10, b = 0.93 и, следовательно, искомая линия регрессии
y = ax + b = 2.10x + 0.93.
Второй способ — использование функции ЛИНЕЙН (возвращает значения a и b, вычисленные методом наименьших квадратов).
Этот способ требует аккуратного выполнения правил работы с функцией ЛИНЕЙН.
Ниже приведено изображение фрагмента листа Excel с решением задачи.
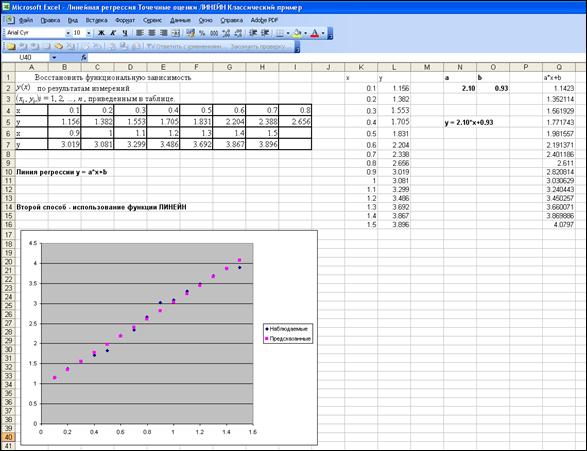
Получили a = 2.10, b = 0.93 и, следовательно, искомая линия регрессии
y = ax + b = 2.10x + 0.93.
Третий способ — использование процедуры «Регрессия» пакета «Анализ данных» обсудим позже, поскольку эта процедура автоматически вычисляет статистические свойства точечных оценок коэффициентов регрессии и характеристики качества модели, которые обсуждаются разделе «Доверительные интервалы коэффициентов регрессии».
Пример 2
Пример 2.
Управляющий сетью магазинов планирует открыть несколько новых магазинов. Он полагает, что объёмы продаж напрямую зависит от величин торговых площадей. Ваша задача разработать статистическую модель, позволяющую прогнозировать объёмы продаж в зависимости от величины торговых площадей новых магазинов.
Вы располагаете данными (данные приведены в таблице, площадь указана в сотнях квадратных метров, объём годовых продаж — в млн. рублей) о размере годовых продаж четырнадцати магазинов и знаете величины торговых площадей этих магазинов.
Номер магазина |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
Площадь |
1.7 |
1.6 |
2.8 |
5.6 |
1.3 |
2.2 |
1.3 |
1.1 |
3.2 |
1.5 |
5.2 |
4.6 |
5.8 |
2.3 |
Объём продаж |
3.7 |
3.9 |
6.7 |
9.5 |
3.4 |
5.6 |
3.7 |
2.7 |
5.5 |
2.9 |
10.7 |
7.6 |
11.8 |
4.1 |
Ниже приведено изображение фрагмента листа Excel с решением задачи.
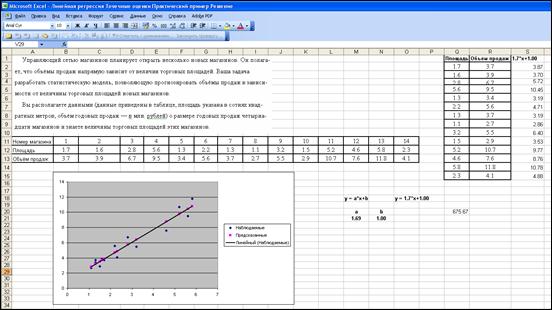
Получили
Объём годовых продаж = 1.69* (размеры торговых площадей) + 1, объёмы продаж измерены в миллионах рублей, размеры торговых площадей — в сотнях квадратных метров,
или: y = 1.69x + 1.00, где y – объёмы продаж в миллионах рублей, x – размеры торговых площадей — в сотнях квадратных метров.