5. 2. Доверительные интервалы для коэффициентов регрессии
В некотором эксперименте измерены значения пары случайных величин y и x
(x1, y1), (x2, y2), …(xn, yn).
Без ограничения общности можно считать, что величина x измерена точно, в то время как измерение величины y содержит случайные погрешности. Это означает, что погрешность измерения величины x пренебрежимо мала по сравнению с погрешностью измерения величины y. Таким образом, результаты эксперимента можно рассматривать как выборочные значения случайной величины h(x), зависящей от x как от параметра.
Пусть требуется построить зависимость y(x).
Регрессией называют зависимость условного математического ожидания величины h(x) от x:
![]() .
.
Задача регрессионного анализа состоит в восстановлении по результатам измерений {(xi,yi)}, i = 1, 2, …, n функциональной зависимости y(x).
Аппроксимируем искомую зависимость y(x) функцией f(x; a0, a1, …, ak).
Это означает, что результаты измерений можно представить в виде
![]() ,
,
где a0, a1, …, ak — неизвестные параметры регрессии, а ei — случайные величины, характеризующие погрешности эксперимента.
Обычно предполагается, что ei — это независимые нормально распределенные случайные величины с M(ei) = 0 и одинаковыми дисперсиями D(ei) = s2.
В случае простейшей линейной регрессии выдвигается гипотеза о том, что функция f(x; a0, a1, …, ak) зависит от двух параметров и имеет вид ![]() ,
, ![]() .
.
Точечные оценки параметров регрессии известны, они вычисляются по формулам
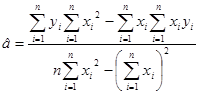 ,
, 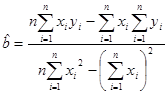 .
.
M(ei) = 0, D(ei) = s2 обычно неизвестна, её оценку s2 можно получить, например, методом максимального правдоподобия:
![]() .
.
Оценки ![]() — несмещенные состоятельные оценки параметров регрессии
— несмещенные состоятельные оценки параметров регрессии ![]() .
.
Важно понимать, что точечные оценки ![]() — случайные величины, о которых известно, что они распределены нормально с математическими ожиданиями
— случайные величины, о которых известно, что они распределены нормально с математическими ожиданиями ![]() и дисперсиями
и дисперсиями 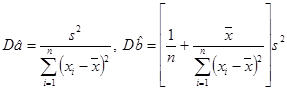 .
.
Используя информацию о статистических свойствах оценок ![]() , можно построить доверительные интервалы для оцениваемых параметров s2, a, b.
, можно построить доверительные интервалы для оцениваемых параметров s2, a, b.
Доверительный интервал для константы b
Если дисперсия s2 известна, то случайная величина
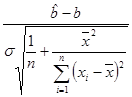
имеет стандартное нормальное распределение и доверительный интервал
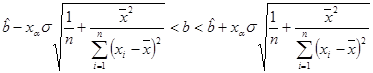
накрывает неизвестный параметр b с вероятностью 1– a. Здесь критическая точка xa — решение уравнения ![]() , где
, где ![]() — функция Лапласа.
— функция Лапласа.
Если дисперсия s2 неизвестна, то используем её оценку ![]() , в качестве критерия можно взять величину
, в качестве критерия можно взять величину
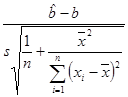 ,
,
она имеет распределение Стьюдента с (n – 2) степенями свободы и доверительный интервал
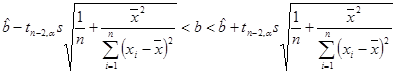
накрывает неизвестный параметр b с вероятностью 1– a.
Здесь критическая точка tn- 2, a — корень уравнения ![]() , Fn-2(tn- 2, a )— функция распределения Стьюдента с (n – 2) степенями свободы. Величину
, Fn-2(tn- 2, a )— функция распределения Стьюдента с (n – 2) степенями свободы. Величину ![]() — стандартную ошибку регрессии, вычисляют по формуле
— стандартную ошибку регрессии, вычисляют по формуле ![]() :
:
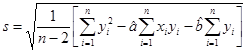 .
.
Для того чтобы найти границы доверительного интервала, задаём малое значение a,
находим соответствующую критическую точку, затем вычисляем точечную оценку ![]() параметра b и наконец — границы соответствующего доверительного интервала.
параметра b и наконец — границы соответствующего доверительного интервала.
Доверительный интервал для наклона a
Если дисперсия s2 известна, то случайная величина
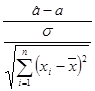
имеет стандартное нормальное распределение.
Если a — доверительная вероятность, и критическая точка xa — решение уравнения
![]() , где Φ(x) — функция Лапласа, то доверительный интервал
, где Φ(x) — функция Лапласа, то доверительный интервал
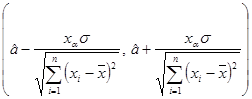
накрывает оцениваемый параметр a с вероятностью 1– a.
Если же дисперсия неизвестна, то в качестве критерия можно взять величину
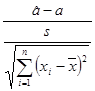 ,
,
она имеет распределение Стьюдента с (n – 2) степенями свободы и поэтому интервал
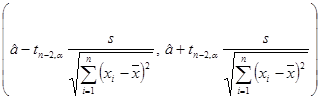
накрывает оцениваемый параметр a с доверительной вероятностью 1– a.
Здесь критическая точка tn- 2, a — корень уравнения ![]() , где F(tn- 2, a) — функция распределения Стьюдента с (n – 2) степенями свободы.
, где F(tn- 2, a) — функция распределения Стьюдента с (n – 2) степенями свободы.
Для того чтобы найти границы доверительного интервала, задаём малое значение a,
находим соответствующую критическую точку, затем вычисляем точечную оценку ![]() параметра a и наконец — границы доверительного интервала.
параметра a и наконец — границы доверительного интервала.
Доверительный интервал для дисперсии
Интервал 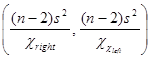 накрывает неизвестную дисперсию s2 с доверительной вероятностью 1– a.
накрывает неизвестную дисперсию s2 с доверительной вероятностью 1– a.
Здесь критические точки ![]() и
и ![]() — решения уравнений
— решения уравнений ![]() и
и ![]() , где Fn-2(x)— функция распределения
, где Fn-2(x)— функция распределения ![]() с (n – 2) степенями свободы.
с (n – 2) степенями свободы.
Для того чтобы найти границы доверительного интервала, задаём малое значение a, находим критические точки, затем вычисляем точечную оценку ![]() параметра
параметра ![]() и наконец — границы соответствующего доверительного интервала.
и наконец — границы соответствующего доверительного интервала.
Внимание!
Функция Excel СТЬЮДРАСПОБР(p, k) возвращает значение t, при котором P(|x| > t) = p, x — значение случайной величины, имеющей распределение Стьюдента с k степенями свободы. Поэтому решение уравнения 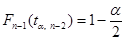 в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 2).
в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 2).
В Excel функция распределения случайной величины определена нестандартно: Fx(x) = P(x >x). Поэтому решение уравнения 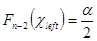 возвращает функция ХИ2ОБР(1–a/2, n – 2) , а решение уравнения
возвращает функция ХИ2ОБР(1–a/2, n – 2) , а решение уравнения 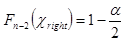 — ХИ2ОБР(a/2, n – 2).
— ХИ2ОБР(a/2, n – 2).
Пример 1
Пример 1. В таблице приведены некоторые экспериментальные данные:
x |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
y |
1.156 |
1.382 |
1.553 |
1.705 |
1.831 |
2.204 |
2.388 |
2.656 |
x |
0.9 |
1.0 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
|
y |
3.019 |
3.081 |
3.299 |
3.486 |
3.692 |
3.867 |
3.896 |
|
Требуется найти доверительные интервалы параметров a и b регрессии y (x)= ax + b и доверительный интервал для дисперсии s2.
В Excel доверительные интервалы параметров регрессии a и b можно вычислить двумя способами: вычислением по формуле или с помощью процедуры «Регрессия» пакета «Анализ данных».
Первый способ — вычисление доверительных интервалов по формулам.
Внимание!
Функция Excel СТЬЮДРАСПОБР(p, k) возвращает значение t, при котором P(|x| > t) = p, x — значение случайной величины, имеющей распределение Стьюдента с k степенями свободы. Поэтому решение уравнения ![]() в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 2).
в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 2).
В Excel функция распределения случайной величины определена нестандартно: Fx(x) = P(x >x). Поэтому решение уравнения ![]() возвращает функция ХИ2ОБР(1–a/2, n – 2) , а решение уравнения
возвращает функция ХИ2ОБР(1–a/2, n – 2) , а решение уравнения ![]() — ХИ2ОБР(a/2, n – 2).
— ХИ2ОБР(a/2, n – 2).
. Ниже приведено изображение фрагмента листа Excel с решением задачи.
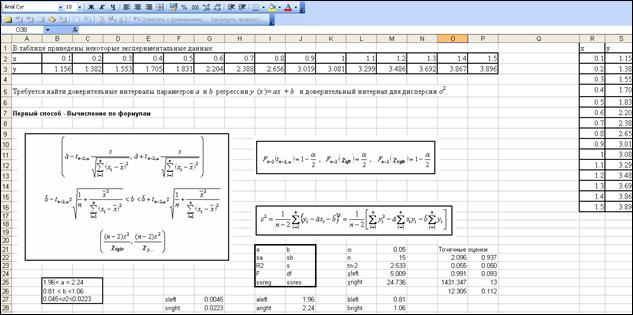
Получили: с доверительной вероятностью 0.95 интервал (1.96, 2.24) накрывает значение параметра регрессии a;
с доверительной вероятностью 0.95 интервал (0.81, 1.06) накрывает значение параметра регрессии b;
с доверительной вероятностью 0.95 интервал (0.045, 0.0223) накрывает значение дисперсии s2.
Второй способ — вычисление доверительных интервалов с помощью процедуры «Регрессия» пакета «Анализ данных».
Ниже приведено изображение фрагмента листа Excel с решением задачи.
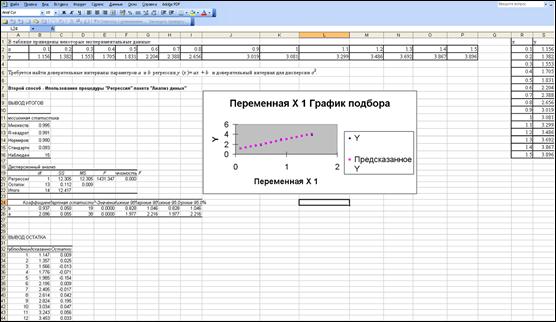
Получили: с доверительной вероятностью 0.95 интервал (1.977, 2.216) накрывает значение параметра регрессии a;
с доверительной вероятностью 0.95 интервал (0.828, 1.046) накрывает значение параметра регрессии b.
Пример 2
Пример 2. Управляющий сетью магазинов планирует открыть несколько новых магазинов. Он полагает, что объёмы продаж напрямую зависит от величин торговых площадей. Ваша задача разработать статистическую модель, позволяющую прогнозировать объёмы продаж в зависимости от величины торговых площадей новых магазинов.
Вы располагаете данными (данные приведены в таблице, площадь указана в сотнях квадратных метров, объём годовых продаж — в млн. рублей) о размере годовых продаж четырнадцати магазинов и знаете величины торговых площадей этих магазинов.
Номер магазина |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
Площадь |
1.7 |
1.6 |
2.8 |
5.6 |
1.3 |
2.2 |
1.3 |
1.1 |
3.2 |
1.5 |
5.2 |
4.6 |
5.8 |
2.3 |
Объём продаж |
3.7 |
3.9 |
6.7 |
9.5 |
3.4 |
5.6 |
3.7 |
2.7 |
5.5 |
2.9 |
10.7 |
7.6 |
11.8 |
4.1 |
Ниже приведено изображение фрагмента листа Excel с решением задачи.
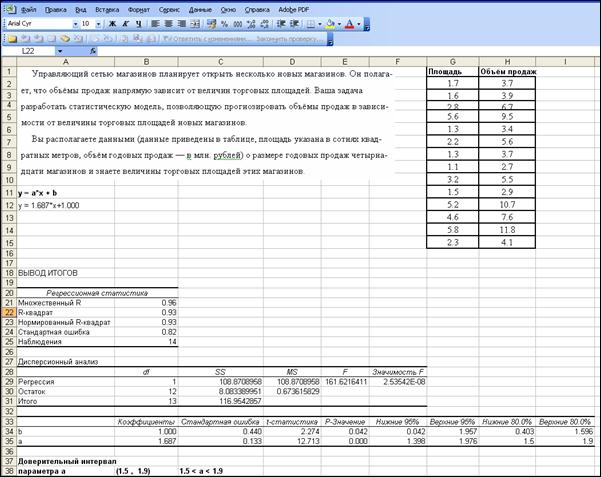
Получили: с доверительной вероятностью 0.8 интервал (1.5, 1.9) накрывает значение параметра регрессии a.
Это означает, что с вероятностью 0.8 можно утверждать: при увеличении торговых площадей на 100 м2 объём продаж возрастёт не менее чем на 1.5 и не более чем на 1.9 миллионов рублей.