5. 3. Доверительные области для регрессии
В некотором эксперименте измерены значения пары случайных величин y и x
(x1, y1), (x2, y2), …(xn, yn).
Без ограничения общности можно считать, что величина x измерена точно, в то время как измерение величины y содержит случайные погрешности. Это означает, что погрешность измерения величины x пренебрежимо мала по сравнению с погрешностью измерения величины y. Таким образом, результаты эксперимента можно рассматривать как выборочные значения случайной величины h(x), зависящей от x как от параметра.
Пусть требуется построить зависимость y(x).
Регрессией называют зависимость условного математического ожидания величины h(x) от x: 
.
Задача регрессионного анализа состоит в восстановлении функциональной зависимости y(x) по результатам измерений {(xi,yi)}, i = 1, 2, …, n.
В случае простейшей линейной регрессии выдвигается гипотеза о том, что функция f(x; a0, a1, …, ak) имеет вид
f(x; a, b)= ax + b.
Доверительный коридор линии регрессии
Пусть линейная регрессия построена: 
.
Возьмем в области изменения аргумента некоторую точку x0 и вычислим
.
Эта величина случайная и меняется от выборки к выборке.
Ее математическое ожидание равно истинному значению функции f(x) в точке x0, величине y0 = a x0+ b.
Доверительный коридор линии регрессии — интервал
,
накрывающий истинное значение величины y0 с вероятностью 1– a.
Величина tn- 2, a — корень уравнения 
, где F(tn- 2, a) — функция распределения Стьюдента с (n – 2) степенями свободы.
Внимание! Функция Excel СТЬЮДРАСПОБР(p, k) возвращает значение t, при котором P(|x| > t) = p, x — значение случайной величины, имеющей распределение Стьюдента с k степенями свободы. Поэтому решение уравнения 
в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 2).
Важно понимать, что доверительный коридор не является доверительной областью для всей линии регрессии — он определяет только концы доверительных интервалов для y при каждом значении x. С помощью коридора регрессии нельзя, например, построить одновременно два доверительных интервала в различных точкахx0 и x1. Такие доверительные интервалы можно построить с помощью доверительной полосы всей линии регрессии.
Пример 1
Пример 1. В таблице приведены некоторые экспериментальные данные:
x |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
y |
1.156 |
1.382 |
1.553 |
1.705 |
1.831 |
2.204 |
2.388 |
2.656 |
x |
0.9 |
1.0 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
|
y |
3.019 |
3.081 |
3.299 |
3.486 |
3.692 |
3.867 |
3.896 |
|
Построим доверительный коридор линии регрессии y (x)= ax + b.
В Excel все эти вычисления можно выполнить, используя процедуру «Регрессия» пакета «Анализ данных» и «Описательные статистики».
Прежде чем приступать к вычислениям в Excel, перепишем формулы для границ доверительного коридора в удобном для работы виде.
Легко убедиться, что границы коридора можно записать в виде
,
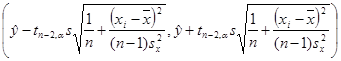где s – стандартное отклонение остатков, 
– выборочная дисперсия переменной x. Значения s и sx вычисляются в Excel процедурой «Описательные статистики».
Важно также помнить, что решение уравнения 
в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 2).
На приведенном ниже рисунке изображён фрагмент листа Excel , содержащий все вычисления.
Пример 2
Пример 2. Управляющий сетью магазинов планирует открыть несколько новых магазинов. Он полагает, что объёмы продаж напрямую зависит от величин торговых площадей. Ваша задача разработать статистическую модель, позволяющую прогнозировать объёмы продаж в зависимости от величины торговых площадей новых магазинов.
Вы располагаете данными о размере годовых продаж четырнадцати магазинов и знаете величины торговых площадей этих магазинов.
Данные приведены в таблице.
Номер магазина |
Площадь (в сотнях м2) |
Объём продаж (выручка в десятках тыс. рублей) |
1 |
1.7 |
3.7 |
2 |
1.6 |
3.9 |
3 |
2.8 |
6.7 |
4 |
5.6 |
9.5 |
5 |
1.3 |
3.4 |
6 |
2.2 |
5.6 |
7 |
1.3 |
3.7 |
8 |
1.1 |
2.7 |
9 |
3.2 |
5.5 |
10 |
1.5 |
2.9 |
11 |
5.2 |
10.7 |
12 |
4.6 |
7.6 |
13 |
5.8 |
11.8 |
14 |
3.0 |
4.1 |
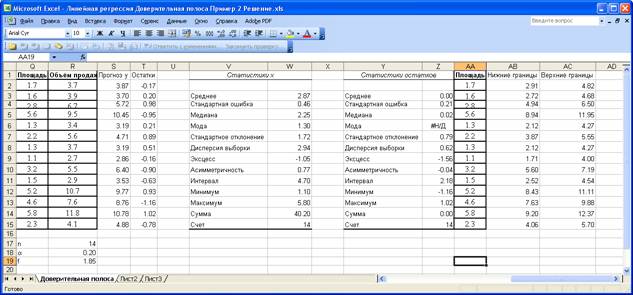
На приведенном ниже рисунке изображён фрагмент листа Excel , содержащий все вычисления.
Доверительная полоса линии регрессии
Пусть линейная регрессия построена: 
.
Доверительная полоса для всей линии регрессии определяется неравенством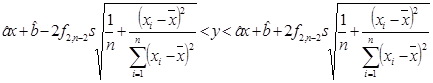 
.
Здесь f2,n-2— корень уравнения 
, Fn-2(x) — функция распределения Фишера с 2 и (n – 2) степенями свободы.
Внимание! В Excel функция распределения случайной величины определена нестандартно: Fx(x) = P(x >x). Поэтому решение уравнения 
возвращает функция FРАСПРОБР(a, n – 2).
С помощью доверительной полосы можно, например, построить одновременно доверительные интервалы для нескольких различных значений переменной x.
Пример 3
В таблице приведены некоторые экспериментальные данные:
x |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
y |
1.156 |
1.382 |
1.553 |
1.705 |
1.831 |
2.204 |
2.388 |
2.656 |
x |
0.9 |
1.0 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
|
y |
3.019 |
3.081 |
3.299 |
3.486 |
3.692 |
3.867 |
3.896 |
|
Легко убедиться, что границы полосы можно записать в виде
,
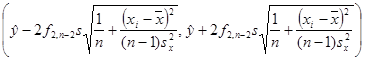где s – стандартное отклонение остатков, 
– выборочная дисперсия переменной x. Значения s и sx вычисляются в Excel процедурой «Описательные статистики».
На приведенном ниже рисунке изображён фрагмент листа Excel , содержащий все вычисления.
Пример 4
Управляющий сетью магазинов планирует открыть несколько новых магазинов. Он полагает, что объёмы продаж напрямую зависит от величин торговых площадей. Ваша задача разработать статистическую модель, позволяющую прогнозировать объёмы продаж в зависимости от величины торговых площадей новых магазинов.
Вы располагаете данными о размере годовых продаж четырнадцати магазинов и знаете величины торговых площадей этих магазинов.
Данные приведены в таблице.
Номер магазина |
Площадь (в сотнях м2) |
Объём продаж (выручка в десятках тыс. рублей) |
1 |
1.7 |
3.7 |
2 |
1.6 |
3.9 |
3 |
2.8 |
6.7 |
4 |
5.6 |
9.5 |
5 |
1.3 |
3.4 |
6 |
2.2 |
5.6 |
7 |
1.3 |
3.7 |
8 |
1.1 |
2.7 |
9 |
3.2 |
5.5 |
10 |
1.5 |
2.9 |
11 |
5.2 |
10.7 |
12 |
4.6 |
7.6 |
13 |
5.8 |
11.8 |
14 |
3.0 |
4.1 |
На приведенном ниже рисунке изображён фрагмент листа Excel , содержащий все вычисления.
