Процедура "Регрессия" пакета "Анализ данных"

Процедура «Регрессия» пакета «Анализ данных»

Процедура решает простейшую задачу парной линейной регрессии:

  – по заданным значениям  , i =1, 2, …, n  строит методом наименьших квадратов линейную функцию регрессии ;

– вычисляет некоторые статистики для анализа качества аппроксимации.

Исходные данные для функции

— выборочные значения , i =1, 2, …, n  

Содержание отчёта о вычислениях, которые выполняются процедурой, определяется пользователем.

Основные численные результаты представлены в трёх таблицах под общим заголовком

 

ВЫВОД ИТОГОВ

 

Регрессионная статистика
Множественный R
R-квадрат
Нормированный R-квадрат
Стандартная ошибка
Наблюдения

 

 

Здесь:

 

R-квадрат – коэффициент детерминации:   ;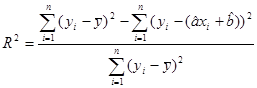

Стандартная ошибка  — стандартная ошибка регрессии:  ,     ;

Наблюдения —  количество наблюдений n.

 

 

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия
Остаток
Итого

 

В двух строках таблицы отображаются статистики, относящиеся соответственно к регрессии и к остаткам регрессии:

df — число степеней свободы: ;

SS — сумма квадратов регрессии: ;

MS — среднее суммы квадратов регрессии, сумма квадратов, делённая на число переменных m, в данном случае m = 1.

F — значение критерия Фишера: ;

Значимость F —  вычисленное по выборке значение плотности вероятности распределения Фишера с (1, n-2) степенями свободы;

Следующая таблица — основная таблица, описывающая линию регрессии.

 

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение
Переменная X 1

 

Нижние 95%	Верхние 95%	Нижние p%	Верхние p%

 

В двух строках таблицы отображаются статистики, относящиеся соответственно к константе b (Y-пересечение) и к коэффициенту a  (Переменная X 1) в уравнении линии регрессии y = ax + b:

Коэффициенты — значения коэффициентов соответственно b  и a  в уравнении линии регрессии y = ax + b;

 Стандартная ошибка— стандартная ошибка регрессии:  , ;

t-статистика — вычисленное по выборке значение критерия Стьюдента для проверки значимости коэффициентов (нулевая гипотеза – коэффициент равен нулю): точечная оценка коэффициента, делённая на его стандартную ошибку: ;

P-Значение значение плотности вероятности распределения Стьюдента  с (n-2) степенями свободы (малые значения вероятности свидетельствуют в пользу значимости коэффициентов).

Нижние 95%, Верхние 95%, Нижние 90.0%, Верхние 90.0% — соответственно нижние и верхние границы доверительных интервалов для коэффициентов b  и a (границы вычисляются с 95% доверительной вероятностью вычисляются по умолчанию,  и с p%, заданной пользователем).

На приведенном ниже рисунке можно видеть решение задачи для различных типов аппроксимирующих функций.