Пример 1. Задана выборка, содержащая 150 значений случайной величины, о которой известно, что она имеет нормальное распределение с известной дисперсией Dx = s² = 0.36  и неизвестным математическим ожиданием Mx.

Найдём 95% доверительный интервал для неизвестного математического ожидания Mx.

На приведенном ниже рисунке изображён фрагмент листа Excel с результатами вычислений.

В результате получили  95% доверительный интервал (-0.15, 0.04) неизвестного математического ожидания нормально распределённой случайной величины. Дисперсия распределения равна 0.36.

Доверительные интервалы для математического ожидания нормально распределённой случайной величины с неизвестной дисперсией

Пусть x — нормально распределенная случайная величина с неизвестным математическим ожиданием a и неизвестной дисперсией s², представленная выборочными значениями

x₁, x₂, …, x_n.

Задача состоит в построении доверительного интервала для неизвестного математического ожидания a.

В качестве оценки параметра a возьмем выборочное среднее .

В качестве оценки неизвестной дисперсии возьмём .

Относительно случайной величины  известно:

• случайная величина   распределена нормально и ее математическое ожидание равно a, ;
• случайная величина  тоже распределена нормально и ее математическое ожидание равно нулю, ;
• дисперсия случайной величины  равна ;
• случайная величина  распределена по закону Стьюдента с (n-1) степенями свободы.

Таким образом построен «агрегат», случайная функция выборочных значений

,

которая представляет собой случайную величину с известным распределением — распределением Стьюдента с (n-1) степенями свободы. Распределение Стьюдента не зависит ни от оцениваемого параметра a, ни от единиц измерения выборочных значений.

Получен универсальный алгоритм построения доверительных интервалов для неизвестного математического ожидания при неизвестной дисперсии.

Пусть F_n-1(t)  — функция распределения Стьюдента с (n-1) степенями свободы. Зададимся доверительной вероятностью 1-a  и определим величину t_{a,,n -1} из уравнения .

Строим доверительный интервал . Этот интервал с вероятностью 1-a  накрывает оцениваемый параметр a, т.е. неравенство  

выполняется с вероятностью 1-a .

Т.е. в данном случае ,  .

Пример 2. Задана выборка, содержащая 150 значений случайной величины, о которой известно, что она имеет нормальное распределение с неизвестной дисперсией  и неизвестным математическим ожиданием Mx.

Найдём 95% доверительный интервал для неизвестного математического ожидания Mx.

На приведенном ниже рисунке изображён фрагмент листа Excel с результатами вычислений.

Важно знать, что функция Excel СТЬЮДРАСПОБР(p, k)  возвращает значение t, при котором P(|x| > t) = p, x — значение случайной величины, имеющей распределение Стьюдента с k  степенями свободы.

Поэтому решение уравнения  в Excel возвращает функция СТЬЮДРАСПОБР(a, n – 1). 

В результате получили  интервальную оценку неизвестного математического ожидания нормально распределённой случайной величины, с вероятностью 0.95 истинное значение математического ожидания накрывается интервалом (-0.14, 0.04).

Доверительные интервалы для дисперсии нормально распределённой случайной величины с известным математическим ожиданием

Пусть x — нормально распределенная случайная величина с известным математическим ожиданием Mx = a и неизвестной дисперсией s², представленная выборочными значениями

x₁, x₂, …, x_n.

Задача состоит в построении доверительного интервала для неизвестной дисперсии s².

В качестве оценки неизвестной дисперсии возьмём .

Поскольку каждая из случайных величин  имеет стандартное нормальное распределение, то случайная величина  имеет  распределение c² с n степенями свободы.

Для построения доверительного интервала зададимся доверительной вероятностью a и определим величины c²_{left, n} и c²_{right, n} . Квантили c²_left,_n и c²_right,n находятся как корни уравнений  и , где F_n(x) — функция распределения c² с n степенями свободы.

Доверительный интервал для дисперсии

Для c²_{left, n} и c²_{right, n}  выполнены условия

 ,  , , и, следовательно,

.

Имеем доверительный интервал для неизвестной дисперсии нормально распределённой случайной величины с известным математическим ожиданием Mx = a

.

Пример 3. Задана выборка, содержащая 150 значений случайной величины, о которой известно, что она имеет нормальное распределение с известным математическим ожиданием Mx =3.

Найдём 90% доверительный интервал для неизвестной дисперсии Dx = s² .

В Excel функция распределения случайной величины определена нестандартно: F_x(x) = P(x > x). Поэтому для вычисления квантиля  вводим  в качестве аргумента функции ХИ2ОБР значение вероятности, равное , а для вычисления  – .

На приведенном ниже рисунке изображён фрагмент листа Excel с результатами вычислений.

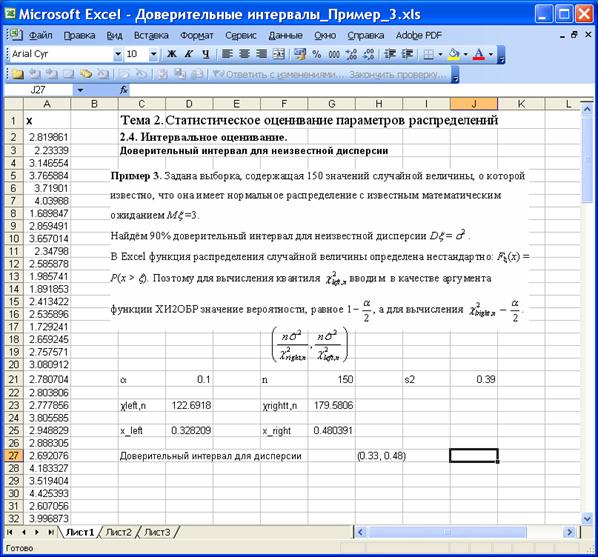
С доверительной вероятностью 0.90 можно утверждать: истинное значение дисперсии Dx  нормально распределенной случайной величины x  c известным математическим ожиданием Mx =3  представленной 150-ю выборочными значениями, покрывается интервалом (0.33, 0.48).

Доверительные интервалы для дисперсии нормально распределённой случайной величины с неизвестным математическим ожиданием

Пусть x — нормально распределенная случайная величина с неизвестным математическим ожиданием Mx = a и неизвестной дисперсией s², представленная выборочными значениями

x₁, x₂, …, x_n.

Задача состоит в построении доверительного интервала для дисперсии s².

В качестве оценки неизвестной дисперсии возьмём . Здесь — оценка неизвестного математического ожидания.

Можно доказать, что случайная величина  имеет c² распределение с (n-1) степенями свободы.

Для построения доверительного интервала зададимся доверительной вероятностью a и определим величины c²_{left, n} и c²_{right, n} . Квантили c²_left,_n и c²_right,n находятся как корни уравнений  и , где F_n(x) — функция распределения c² с (n-1) степенями свободы.

Тогда

,  , и

Имеем доверительный интервал для неизвестной дисперсии нормально распределённой случайной величины с неизвестным математическим ожиданием

Пример 4. Задана выборка, содержащая 150 значений случайной величины, о которой известно, только, что она имеет нормальное распределение.

Найдём 90% доверительный интервал для неизвестной дисперсии Dx = s² .

В Excel функция распределения случайной величины определена нестандартно: F_x(x) = P(x > x). Поэтому для вычисления квантиля c²_{left, n} вводим  в качестве аргумента функции ХИ2ОБР значение вероятности, равное .

На приведенном ниже рисунке изображён фрагмент листа Excel с результатами вычислений.

С доверительной вероятностью 0.90 можно утверждать: истинное значение дисперсии Dx  нормально распределенной случайной величины x  c известным математическим ожиданием Mx =3  представленной 150-ю выборочными значениями, покрывается интервалом (0.333280, 0.48).

Доверительный интервал для параметра

Пуассоновского распределения

Пусть x — случайная величина, имеющая распределение Пуассона  с неизвестным параметром  l представлена выборочными значениями x₁, x₂, …, x_n,

, i=1, 2, …, n, Mx = l, .

Задача состоит в построении доверительного интервала для параметра  l.

Точечная оценка параметра l и её статистические характеристики известны:

 ,   , .

Известно также, что случайная величина  асимптотически распределена нормально с параметрами 0 и 1, т.е. при n® ¥ стремится к случайной величине со стандартным нормальным распределением.

Тогда, если x_a — решение уравнения , где F(x)— функция Лапласа, то  

и можно записать доверительный интервал для l:

,

который с доверительной вероятностью P @ 1-a  накрывает оцениваемый параметр Пуассоновского распределенияl.

Пример 5. Заданы три выборки содержащие соответственно 20, 50 и 100  значений случайной величины, о которой известно, что она имеет распределение Пуассона с неизвестным параметром l.

Выборочные значения  2, 3, 1, 1, 1, 5, 2, 5, 3, 3, 2, 4, 2, 1, 1, 2, 3, 4, 3, 3, n = 20,

4, 3, 1, 8, 4, 5, 2, 4, 5, 0, 5, 0, 0,  4, 3, 1, 1, 2, 5, 2, 1, 0, 0, 2, 1, 0, 1, 4, 5, 3, 1, 2, 3, 1, 6, 1, 2, 5, 3, 6, 4, 2, 2, 1, 2, 1, 3, 3, 4, 5, n = 50

и

3, 3, 2, 5, 3, 5, 3, 1, 4, 1, 6, 4, 1, 2, 0, 3, 5, 2, 2, 3, 4, 3, 3, 8, 3, 4, 2, 2, 2, 3, 1, 4, 2, 2, 1, 6, 1, 2, 2, 2, 6, 4, 2, 5, 3, 6, 3, 4, 6, 3, 8, 3, 4, 3, 3, 6, 4, 3, 4, 8, 3, 3, 5, 2, 5, 2, 1, 4, 3, 2, 4, 3, 2, 4, 1, 3, 4, 3, 5, 3, 1, 2, 1, 5, 6, 3, 1, 4, 1, 2, 4, 3, 1, 1, 3, 6, 3, 4, 5, 4, n = 100,

Найдём 95% доверительный интервал для неизвестного математического ожидания Mx. Напоминаем, что Mx = l, т.е. речь идёт об интервальной оценке параметра распределения Пуассона.

На приведенном ниже рисунке изображён фрагмент листа Excel с результатами вычислений.

С доверительной вероятностью 0.95 можно утверждать: истинное значение параметра λ случайной величины,  имеющей распределение Пуассона, представленной 20-ю выборочными значениями, покрывается интервалом (1.90, 3.30), для выборки объёма 50 доверительный интервал  – (2.25, 3.15), для выборки объёма сто – (2.89, 3.59).

Доверительный интервал для вероятности

В практических задачах достаточно часто возникает необходимость строить доверительные интервалы для оценки неизвестной вероятности события, которое может произойти или не произойти в одном из независимых экспериментов.

Точечная оценка вероятности события в серии из n  независимых испытаний Бернулли вычисляется по формуле , где m — число появлений события в серии.

Если x_a — решение уравнения ,  где F(x) — функция Лапласа, то с вероятностью P@1-a  неизвестный параметр p накрывается интервалом

.

Построенный доверительный интервал обладает естественным свойством — его ширина уменьшается с ростом объема выборки .

Если же при постоянном объеме выборки увеличивать доверительную вероятность, то ширина доверительного интервала будет возрастать.

Однако формулы для границ этого интервала устроены так, что доверительный интервал всегда остается внутри отрезка [0, 1].

Пример 6. Проведено 20 независимых испытаний с неизвестной вероятностью успеха в каждом из них. Достигнуто 6  успехов.

Найдем 95% доверительный интервал для неизвестной вероятности p.

На приведенном ниже рисунке изображён фрагмент листа Excel с результатами вычислений.

С доверительной вероятностью 0.95 можно утверждать, что истинное значение вероятности накрывается интервалом (0.12, 0.51).

Пример 7. Проведено 15 серий независимых испытаний с неизвестной вероятностью успеха в каждом из них. В каждой серии проводилось  испытаний и было достигнуто  успехов.

Вычислим для каждой серии 95% доверительный интервал для неизвестной вероятности  и изобразим результаты графически. Данные — значения  и  приведены в таблице.

На приведенном ниже рисунке изображён фрагмент листа Excel с результатами вычислений.

Результаты полностью подтверждают утверждение о том, что с увеличением числа испытаний возрастает точность интервальных оценок.

Доверительный интервал для коэффициента корреляции

Пусть (x, h) — двумерный случайный вектор, представленный выборкой  объема n

(x₁, y₁), (x₂, y₂), …, (x_n, y_n).

Задача состоит в построении доверительного интервала для коэффициента корреляции.

Точечная оценка коэффициента корреляции k_xh  является выборочный коэффициент корреляции , который вычисляется по формуле

.

Здесь

, , ,

 и .

Если  x_a — решение уравнения , то доверительный интервал, накрывающий коэффициент корреляции k_xh  с вероятностью  определяется следующим образом:

 ,.

где — гиперболический косинус, arth x — функция, обратная гиперболическому тангенсу, которая определяется как решение уравнения th y = x формулой .

Формулы устроены таким образом, что доверительный интервал всегда остается внутри отрезка [-1, 1], что соответствует теоретическим представлениям о коэффициенте корреляции, как о величине, не превышающей по абсолютной величине  единицу —   | k_xh | £ 1.

Пример 8. Задана выборка, содержащая 10 значений двумерного случайного вектора (x, h)

Найдём 95% доверительный интервал для коэффициента корреляции.

На приведенном ниже рисунке изображён фрагмент листа Excel с результатами вычислений.

С вероятностью 0.950 можно утверждать, что истинное значение коэффициента корреляции принадлежит интервалу (-0.58, 0.68).