Точечные оценки параметров распределений

Пример 1. Задана выборка, содержащая 100 значений случайной величины.

Вычислим точечные оценки математического ожидания и дисперсии случайной величины.

На приведенном ниже рисунке изображён фрагмент листа Excel с вычислениями.

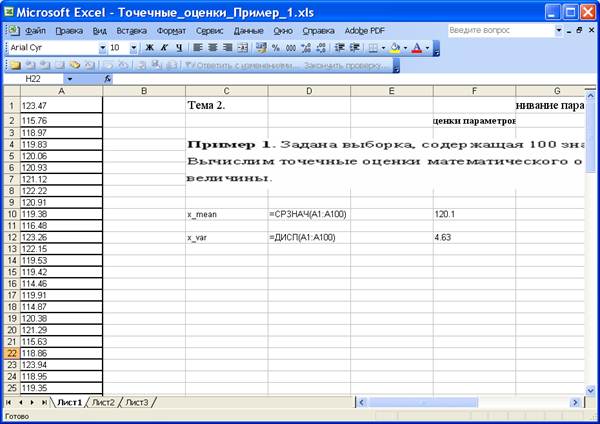
Получили .

Точечная оценка вероятности события

Предположим, что в некотором эксперименте событие A происходит (благоприятный исход испытания) с вероятностью p и не происходит с вероятностью q =1– p и пусть случайная величина  m — количество  благоприятных исходов в серии испытаний. Задача состоит в получении по результатам серии n случайных экспериментов оценки  неизвестного параметра  распределения p.

При заданном числе испытаний n  величина m — случайная величина, имеющая биномиальное распределение. Если событие A в серии из n независимых испытаний произошло m раз, то m — значение случайной величиныm.

Оценку  величины  будем вычислять по формуле .

Эта оценка несмещённая, состоятельная и эффективная.

Доказано, что эта оценка эффективна — обладает при прочих равных условиях минимальной дисперсией.

На рисунке приведен график зависимости точечной оценки вероятности p числа успехов от числа испытаний n в серии испытаний Бернулли. График построен по выборке 1000 значений случайной величины, имеющей биномиальное распределение с параметром p = 0.4. Видно, что с ростом числа испытаний точечная оценка приближается к известному точному значению параметра, которое равно 0.4.

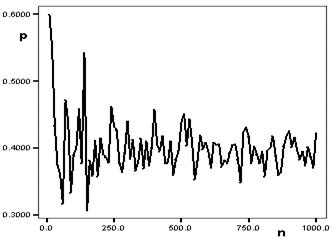
График зависимости точечной оценки вероятности от числа испытаний

Пример 2. Задана выборка, содержащая  20 значений случайной величины (значения m) — количество успехов в эксперименте из 1000 независимых испытаний (проведено 20 одинаковых экспериментов по 1000 независимых испытаний в каждом).

Найдём точечную оценку  вероятности успеха  p и исследуем статистические свойства этой оценки.

На приведенных ниже рисунках изображены фрагменты листа Excel с вычислениями.

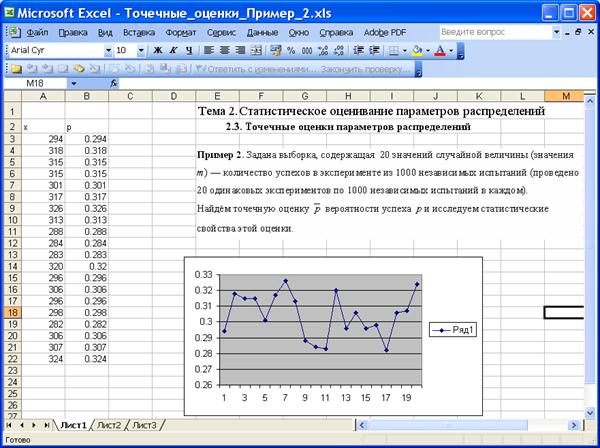
Вычисленные значения оценки вероятности записаны в столбце B. Видно, что все эти значения близки к 0.3.

Значения вероятности  лежат в интервале [0.2672, 0.3525], . Можно достаточно уверенно полагать вероятность успеха равной 0.3.

Точечная оценка параметров равномерного распределения

Пусть  выборка из генеральной совокупности, соответствующей случайной величине x, имеющей равномерное распределение на [0, q ] с неизвестным параметром q. Наша задача — оценить этот неизвестный параметр.

Для случайной величины  x , имеющей равномерное распределение на [0, q] математическое ожидание и дисперсия известны:  и .

А поскольку оценка  величины Mx  известна, , то за оценку  параметра  q можно взять оценку .

Несмещенность оценки очевидна: .

Состоятельность:

 ,

т.е. при n® ¥ дисперсия оценки  стремится к нулю.

Для получения другой оценки  параметра  обратимся к другой статистике:  

Пусть .

Найдем функцию распределения случайной величины :

,  для .

Тогда математическое ожидание и дисперсия случайной величины  равны соответственно  и , т.е. оценка  состоятельная, но смещенная.

Однако если вместо  рассмотреть , то  и , — состоятельная и несмещенная оценка.

А поскольку , то оценка  существенно эффективнее оценки . Например, при  разброс оценки  в 33 раза меньше разброса оценки .

Последний пример еще раз показывает, что выбор статистической оценки неизвестного параметра распределения — важная и нетривиальная задача.

Пример 3. Задана выборка, содержащая 100 значений случайной величины, о которой известно, что она имеет равномерное распределение на промежутке [0, q].

Вычислим и сравним три оценки неизвестного параметра q, котрые вычисляются по формулам:

, , .

На приведенном ниже рисунке изображён фрагмент листа Excel с вычислениями.

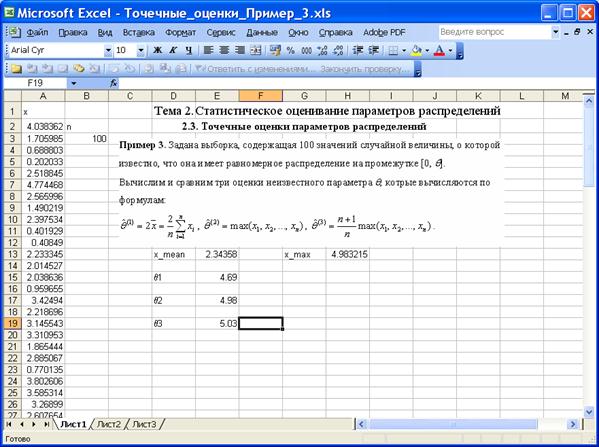
Получили, что оценки  и  близки. Это и понятно, сомножитель  в оценке  при больших  мало отличается от единицы.